题目内容
设定义域为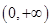 的单调函数
的单调函数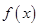 ,对任意的
,对任意的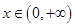 ,都有
,都有 ,若
,若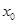 是方程
是方程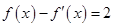 的一个解,则
的一个解,则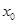 可能存在的区间是( )
可能存在的区间是( )
A.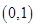 | B.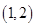 | C. | D.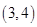 |
B
解析试题分析:由于函数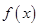 在其定义域
在其定义域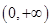 上单调,则存在唯一实数
上单调,则存在唯一实数 使得
使得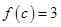 ,对任意的
,对任意的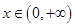 ,都有
,都有 ,则
,则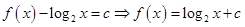 ,由于
,由于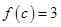 ,
,
因此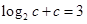 ,因为函数
,因为函数 在区间
在区间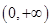 上单调递增,且
上单调递增,且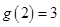 ,所以
,所以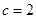 ,故
,故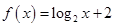 ,令
,令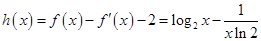 ,则
,则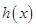 在区间
在区间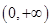 上单调递增,且
上单调递增,且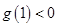 ,
,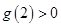 ,故
,故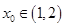 ,故选B.
,故选B.
考点:1.零点存在定理;2.函数的单调性

练习册系列答案
相关题目
已知函数 是定义在
是定义在 上的偶函数,且在区间
上的偶函数,且在区间 上是增函数.令
上是增函数.令 ,
, ,
,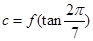 ,则( )
,则( )
A. | B.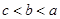 | C.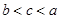 | D.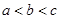 |
在R上定义运算 ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ).
A.{a| } } | B.{a| } } |
C.{a| } } | D.{a| } } |
若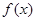 是偶函数,且当
是偶函数,且当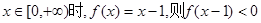 的解集是 ( )
的解集是 ( )
A. | B. | C. | D.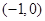 |
下列函数中,既是偶函数又在区间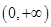 上存在零点的是( )
上存在零点的是( )
A.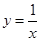 | B.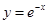 | C.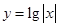 | D.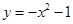 |
如果函数 在
在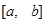 上的最大值和最小值分别为
上的最大值和最小值分别为 、
、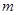 ,那么
,那么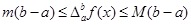 .根据这一结论求出
.根据这一结论求出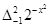 的取值范围( ).
的取值范围( ).
A.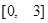 | B.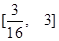  | C. | D.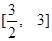 |
设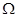 为平面直角坐标系
为平面直角坐标系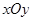 中的点集,从
中的点集,从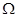 中的任意一点
中的任意一点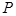 作
作 轴、
轴、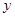 轴的垂线,垂足分别为
轴的垂线,垂足分别为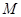 ,
, ,记点
,记点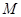 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为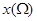 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为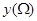 . 若
. 若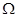 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
①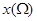 的最大值为
的最大值为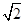 ;
;
②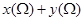 的取值范围是
的取值范围是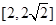 ;
;
③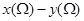 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )
| A.① | B.②③ | C.①② | D.①②③ |
(2013•重庆)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x﹣a)的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 | B.(﹣∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(﹣∞,a)和(c,+∞)内 |
下列函数为偶函数的是
| A.y=sinx | B.y=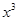 | C.y=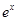 | D.y=ln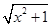 |