题目内容
如果函数 在
在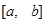 上的最大值和最小值分别为
上的最大值和最小值分别为 、
、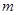 ,那么
,那么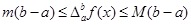 .根据这一结论求出
.根据这一结论求出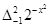 的取值范围( ).
的取值范围( ).
A.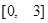 | B.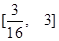  | C. | D.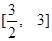 |
B
解析试题分析:函数 在区间
在区间 上最大值为1,最小值为
上最大值为1,最小值为 ,即
,即 ,所以
,所以 ,
, ,即
,即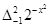 取值范围为
取值范围为 ,选B.
,选B.
考点:新定义概念与函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对任意实数 ,
, 定义运算“⊙”:
定义运算“⊙”: 设
设 ,若函数
,若函数 的图象与
的图象与 轴恰有三个交点,则
轴恰有三个交点,则 的取值范围是( )
的取值范围是( )
A.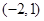 | B. |
C. | D.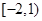 |
函数y=ln(x+1)与 的图像交点的横坐标所在区间为( )
的图像交点的横坐标所在区间为( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
设定义域为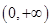 的单调函数
的单调函数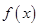 ,对任意的
,对任意的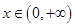 ,都有
,都有 ,若
,若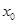 是方程
是方程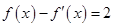 的一个解,则
的一个解,则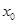 可能存在的区间是( )
可能存在的区间是( )
A.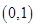 | B.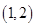 | C. | D.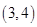 |
设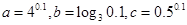 ,则( )
,则( )
A. | B.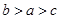 | C. | D.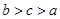 |

 的最大值为( )
的最大值为( )
| A.0 | B.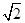 | C.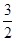 | D. |
(2013•重庆)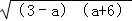 (﹣6≤a≤3)的最大值为( )
(﹣6≤a≤3)的最大值为( )
| A.9 | B.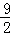 | C.3 | D.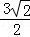 |
设[x]表示不大于x的最大整数, 则对任意实数x, y, 有
| A.[-x]=-[x] |
B.[x +  ]=[x] ]=[x] |
| C.[2x]=2[x] |
D.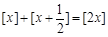 |
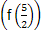 的值是( )
的值是( )
