题目内容
已知数列 的前
的前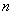 项和
项和 满足
满足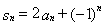 ,
,
(1)求数列 的前三项
的前三项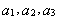
(2)设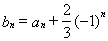 ,求证:数列
,求证:数列 为等比数列,并指出
为等比数列,并指出 的通项公式。
的通项公式。
解:⑴在Sn=2an+(-1)n中分别令n=1,2,3得
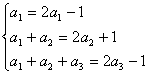 (2分) 解得
(2分) 解得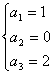 (4分)
(4分)
⑵由Sn=2an+(-1)n,n≥1得Sn-1=2an-1+(-1)n-1,n≥2
两式想减得an=2aa-2an-1+2(-1)n,即an=2an-1-2(-1)n (6分)
∴an+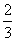 (-1)n=2an-1+
(-1)n=2an-1+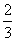 (-1)n-2(-1)n=2an-1+
(-1)n-2(-1)n=2an-1+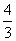 (-1)n-1
(-1)n-1
=2[an-1+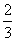 (-1)n-1](n≥2) (9分)
(-1)n-1](n≥2) (9分)
即bn=2bn-1(n≥2),b1=a1-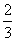 =
=
∴{bn}是首项为 ,公比为2的等比数列. (10分)
,公比为2的等比数列. (10分)
∴bn= ×2n-1= an+
×2n-1= an+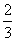 (-1)n
(-1)n
an= ×2n-1-
×2n-1-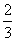 (-1)n (12分)
(-1)n (12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,且满足
,且满足 则
则
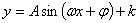 的最大值为
的最大值为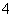 ,最小值为
,最小值为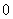 ,最小正周期为
,最小正周期为 ,直线
,直线 是其图像的一条对称轴,则符合条件的解析式为
是其图像的一条对称轴,则符合条件的解析式为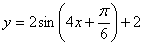 B.
B. 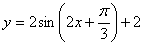
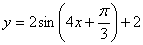 D.
D. 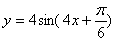
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 最大值为_________________
最大值为_________________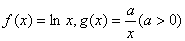 ,设
,设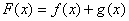
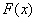 的单调区间
的单调区间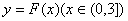 图象上任意一点
图象上任意一点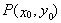 为切点的切线的斜率
为切点的切线的斜率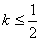 恒成立,求实数
恒成立,求实数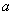 的最小值
的最小值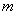 ,使得函数
,使得函数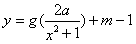 的图象与函数
的图象与函数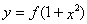 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数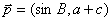 ,
,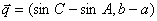 .若
.若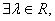 使
使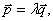 则角C的大小为
则角C的大小为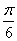 B.
B. 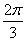 C.
C. 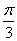 D.
D. 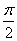
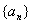 为等比数列,
为等比数列,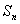 是它的前
是它的前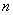 项和。若
项和。若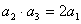 ,且
,且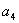 与
与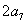 的等差中项为
的等差中项为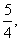 则
则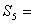 ( )
( ) 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,则角
,则角 范围是( )
范围是( ) B.
B. C.
C. D.
D.