题目内容
已知函数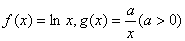 ,设
,设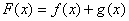
(1)求函数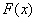 的单调区间
的单调区间
(2)若以函数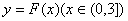 图象上任意一点
图象上任意一点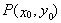 为切点的切线的斜率
为切点的切线的斜率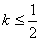 恒成立,求实数
恒成立,求实数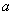 的最小值
的最小值
(3)是否存在实数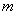 ,使得函数
,使得函数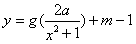 的图象与函数
的图象与函数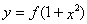 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数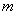 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(Ⅰ)F(x)=f(x)+g(x)=lnx+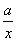 (x>0), =
(x>0), =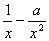 =
=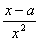
∵a>0,由FF'(x)>0Þx∈(a,+∞),∴F(x)在(a,+∞)上是增函数.
由FF'(x)<0Þx∈(0,a),∴F(x)在(0,a)上是减函数.
∴F(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(Ⅱ)由FF'(x)= 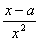 (0<x≤3)得
(0<x≤3)得
k= FF'(x0)= 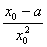 ≤
≤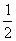 (0<x0≤3)恒成立Ûa≥-
(0<x0≤3)恒成立Ûa≥-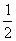 x02+x0恒成立.
x02+x0恒成立.
∵当x0=1时,-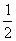 x02+x0取得最大值
x02+x0取得最大值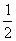
∴a≥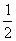 ,a的最小值为
,a的最小值为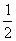 .
.
(Ⅲ)若y=g( )+m-1=
)+m-1=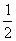 x2+m-
x2+m-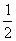 的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点,即
的图像与y=f(1+x2)=ln(x2+1)的图像恰有四个不同交点,即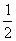 x2+m-
x2+m-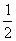 =ln(x2+1)有四个不同的根,亦即m=ln(x2+1)-
=ln(x2+1)有四个不同的根,亦即m=ln(x2+1)-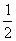 x2+
x2+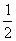 有四个不同的根.令
有四个不同的根.令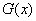 = ln(x2+1)-
= ln(x2+1)-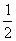 x2+
x2+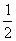 .
.
则GF'(x)=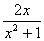 -x=
-x=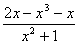 =
=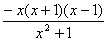
当x变化时GF'(x)、G(x)的变化情况如下表:
| (-¥,-1) | (-1,0) | (0,1) | (1,+¥) | |
| GF'(x)的符号 | + | - | + | - |
| G(x)的单调性 | ↗ | ↘ | ↗ | ↘ |

练习册系列答案
相关题目
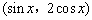 ,b=
,b=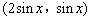 ,设函数
,设函数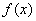 =a
=a b.
b.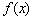 的单调递增区间;
的单调递增区间;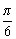 个单位,得到函数
个单位,得到函数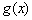 的图象,求函数
的图象,求函数 上的最大值和最小值.
上的最大值和最小值.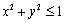 的点
的点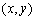 构成的平面区域的面积为
构成的平面区域的面积为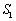 ,满足条件
,满足条件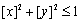 的点
的点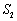 (其中
(其中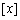 ,
,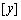 分别表示不大于x,y的最大整数,例如
分别表示不大于x,y的最大整数,例如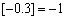 ,
,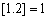 ),给出下列结论:
),给出下列结论: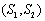 在直线
在直线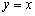 左上方的区域内;
左上方的区域内;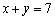 左下方的区域内;
左下方的区域内;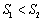 ;
;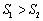 .
.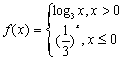 ,则满足方程
,则满足方程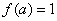 的所有
的所有 的前
的前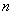 项和
项和 满足
满足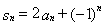 ,
,
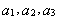
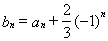 ,求证:数列
,求证:数列 为等比数列,并指出
为等比数列,并指出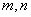 是两条不同的直线,
是两条不同的直线,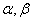 是两个不同
是两个不同 的平面,下列命题中正确的是
的平面,下列命题中正确的是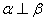 ,
, 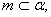
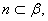 则
则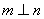
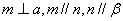 ,则
,则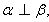
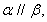
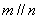
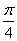 )-sin2(x-
)-sin2(x-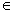 (
(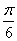 ,
,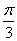 )的值域是_______。
)的值域是_______。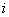 为虚数单位,则
为虚数单位,则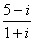 等于
等于
 ,
, ,若向区域
,若向区域 上随机投1个点,这个点落入区域
上随机投1个点,这个点落入区域 的概率
的概率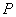 = .
= .