题目内容
已知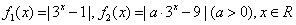 ,且
,且
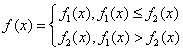
(1)当a=1时,求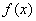 的解析式;
的解析式;
(2)在(1)的条件下,若方程 有4个不等的实根,求实数
有4个不等的实根,求实数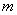 的范围;
的范围;
(3)当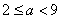 时,设
时,设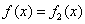 所对应的自变量取值区间的长度为l(闭区间[m,n]的长度定义为
所对应的自变量取值区间的长度为l(闭区间[m,n]的长度定义为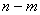 ),试求l的最大值.
),试求l的最大值.
解: (1)当 时,
时, .
.
故

易知当 时
时
所以 -------------------------------------3
-------------------------------------3
(2) ,可画出
,可画出
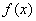 和
和 的图像,
的图像,
由数形结合可知,当 时方程
时方程 有4个不等的实根 -----6
有4个不等的实根 -----6
(3) 当
当 时,因为
时,因为 ,
, ,
,
所以由 ,解得
,解得 ,
,
从而当 时,
时,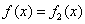
当 时,因为
时,因为 ,
, ,
,
所以由 ,解得
,解得 ,
,
从而当 时,
时,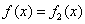
当 时,因为
时,因为 ,
,
从而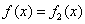 一定不成立
一定不成立
综上得,当且仅当 时,
时,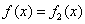 ,
,
故
从而当 时,
时, 取得最大值为
取得最大值为

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
某单位为了解用电量y(度)与气温x(℃)之间的关系,随机抽查了某4天的用电量与当天气温,并制作了对照表:
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程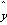 =
=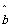 x+
x+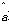 中
中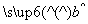 =-2,预测当气温为-4℃时,用电量约为________度.
=-2,预测当气温为-4℃时,用电量约为________度.
 的展开式中含
的展开式中含 的项的系数是 .
的项的系数是 . ≤2x+1≤16},B={x|m+1≤x≤3m-1}.
≤2x+1≤16},B={x|m+1≤x≤3m-1}. 的定义域为
的定义域为 ,则函数
,则函数 的定义域为 ( )
的定义域为 ( ) B.
B. C.
C.  D.
D.
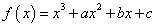 ,在定义域
,在定义域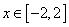 上表示的曲线过原点,且在
上表示的曲线过原点,且在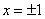 处的切线斜率均为
处的切线斜率均为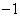 .有以下命题:
.有以下命题: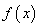 是奇函数;②若
是奇函数;②若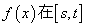 内递减,则
内递减,则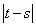 的最大值为4;③
的最大值为4;③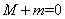 ;④若对
;④若对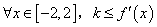 恒成立,则
恒成立,则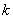 的最大值为2.其中正确命题的个数为 ( )
的最大值为2.其中正确命题的个数为 ( )