题目内容
已知函数 f(x)=a-
(a∈R)在定义域内为奇函数.
(1)确定函数的解析式;
(2)用定义证明f(x)在(-∞,+∞)上是增函数;
(3)求函数f(x)在[1,2]上的值域.
| 2 |
| 2x+1 |
(1)确定函数的解析式;
(2)用定义证明f(x)在(-∞,+∞)上是增函数;
(3)求函数f(x)在[1,2]上的值域.
考点:函数单调性的判断与证明,函数的值域,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:(1)函数f(x)为R上的奇函数,则f(0)=0,即可求得a,进而得到函数式;
(2)运用单调性的定义证明,注意作差和变形、定符号和下结论;
(3)由于函数f(x)在R上递增,则f(x)在[1,2]上递增,求出最小和最大值,即可得到值域.
(2)运用单调性的定义证明,注意作差和变形、定符号和下结论;
(3)由于函数f(x)在R上递增,则f(x)在[1,2]上递增,求出最小和最大值,即可得到值域.
解答:
(1)解:函数f(x)为R上的奇函数,则f(0)=0,
即有a-
=0,解得,a=1,则f(x)=1-
;
(2)证明:设m<n,则f(m)-f(n)=1-
-(1-
)
=
,
由于m<n,则2m<2n,即2m-2n<0,2m>0,2n>0,
则f(m)-f(n)<0,即有函数f(x)在R上递增;
(3)解:由于函数f(x)在R上递增,
则f(x)在[1,2]上递增,即f(1)最小且为1-
=
,
f(2)最大且为1-
=
,
则值域为[
,
].
即有a-
| 2 |
| 20+1 |
| 2 |
| 2x+1 |
(2)证明:设m<n,则f(m)-f(n)=1-
| 2 |
| 2m+1 |
| 2 |
| 2n+1 |
=
| 2(2m-2n) |
| (1+2m)(1+2n) |
由于m<n,则2m<2n,即2m-2n<0,2m>0,2n>0,
则f(m)-f(n)<0,即有函数f(x)在R上递增;
(3)解:由于函数f(x)在R上递增,
则f(x)在[1,2]上递增,即f(1)最小且为1-
| 2 |
| 3 |
| 1 |
| 3 |
f(2)最大且为1-
| 2 |
| 5 |
| 3 |
| 5 |
则值域为[
| 1 |
| 3 |
| 3 |
| 5 |
点评:本题考查函数的奇偶性和单调性的判断和证明,以及运用:求值域,考查运算能力,属于中档题.

练习册系列答案
相关题目
以边长为1的正方形的一条边为旋转轴,旋转一周后所得旋转体侧面积为( )
| A、2π | B、π | C、2 | D、1 |
从装有2个红球和2个黒球的口袋内任取2个球,则互斥而不对立的两个事件是( )
| A、“至少有一个黑球”与“都是红球” |
| B、“至少有一个黒球”与“都是黒球” |
| C、“恰有m个黒球”与“恰有2个黒球” |
| D、“至少有一个黒球”与“至少有1个红球” |
下列函数在(-∞,0)上为增函数的是( )
| A、y=x3 | ||
| B、y=x2 | ||
| C、y=|x| | ||
D、y=(
|
已知f(x)=
,若f(x)为奇函数,则g(-1)的值为( )
|
| A、3 | B、-1 | C、-3 | D、1 |
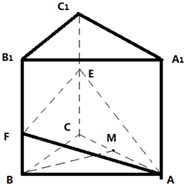 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是