Question

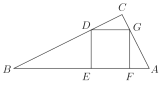
【题目】如图，已知在Rt△ABC中，，，，它的内接正方形DEFG的一边EF在斜边BA上，D、G分别在边BC、CA上，设△ABC的面积为，正方形DEFG的面积为.

（1）试用、分别表示和；

（2）设，求的最大值，并求出此时的.

Answer 1

【答案】（1），；（2），.

【解析】

（1）在直角三角形中，利用，，表示出，从而表示出，在直角三角形和中，分别表示出和，从而表示出正方形的边长，表示出；（2）利用三角恒等变形以及三角函数的性质和基本不等式，计算出的最大值.

（1）在直角三角形中，

，，，

所以，

则的面积

在直角三角形和中

，，

正方形，所以，

所以，即，

所以，其中

（2）根据题意，可得，其中

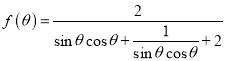
令，

所以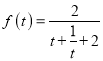

因为，在上单调递减，

所以，

所以

当且仅当，即，时，等号成立.

所以的最大值为，此时.