题目内容
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面 上.用一平行于平面
上.用一平行于平面 的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为
的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为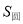 和
和 ,那么
,那么

A.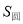
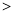
 B.
B.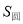 =
= C.
C.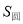
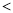
 D.不确定
D.不确定
B
【解析】
试题分析:设球现与圆柱底面的距离为 ,该平面截球所得圆面的半径为
,该平面截球所得圆面的半径为 ,圆的面积为
,圆的面积为
由于圆柱的底面半径与高相等,所以圆环的内圆半径为 ,所以圆环的面积为
,所以圆环的面积为
所以, =
= ,故选B.
,故选B.
考点:空间几何体的结构.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 是偶函数,则k的值是
是偶函数,则k的值是  =_____________.
=_____________.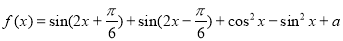 的在区间
的在区间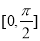 上的最小值为0.
上的最小值为0.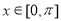 时,求使
时,求使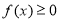 成立的x的集合.
成立的x的集合.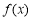 是定义在R上的奇函数,它的图象关于直线
是定义在R上的奇函数,它的图象关于直线 对称,且
对称,且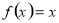
 .若函数
.若函数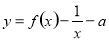 在区间
在区间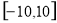 上有10个零点(互不相同),则实数
上有10个零点(互不相同),则实数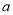 的取值范围是
的取值范围是 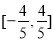 B.
B.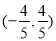 C.
C. D.
D.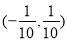
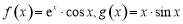 ,其中
,其中 为自然对数的底数.
为自然对数的底数.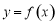 在点
在点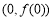 处的切线方程;
处的切线方程; ,不等式
,不等式 恒成立,求实数
恒成立,求实数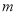 的取值范围;
的取值范围; 时,方程
时,方程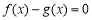 解的个数,并说明理由.
解的个数,并说明理由.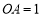 ,在以
,在以 为圆心,以
为圆心,以 为半径的半圆弧上随机取一点B,则
为半径的半圆弧上随机取一点B,则 的面积小于
的面积小于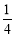 的概率为 .
的概率为 .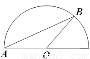
 (
( 且
且 )个单位的药剂,药剂在血液中的含量
)个单位的药剂,药剂在血液中的含量 (克)随着时间
(克)随着时间 (小时)变化的函数关系式近似为
(小时)变化的函数关系式近似为 ,其中
,其中
 个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求
个单位的药剂,要使接下来的2小时中能够持续有效治疗,试求 的最小值.
的最小值. ⊥平面
⊥平面 ,
, ,
,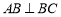 ,
,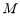 为
为 中点.
中点.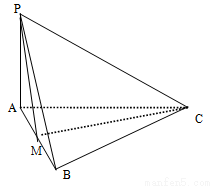
 ;
;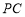 与平面
与平面 所成角的正切值 为
所成角的正切值 为 ,求二面角
,求二面角 -
- -
- 的正弦值.
的正弦值.