题目内容
设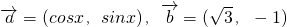
(1)求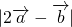 的最大值及相应x的值;
的最大值及相应x的值;
(2)当 •
•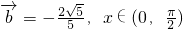 时,求cosx的值.
时,求cosx的值.
解:(1)∵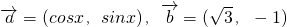
∴ =
=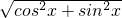 =1,
=1, =
= =2
=2
由此可得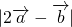 ≤2
≤2 +
+ =4,
=4,
当且仅当2 与
与 共线且反向时,即
共线且反向时,即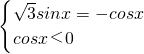 时,等号成立
时,等号成立
解之得:x= +2kπ,k∈Z
+2kπ,k∈Z
综上所述,当x= +2kπ(k∈Z)时,
+2kπ(k∈Z)时,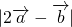 的最大值为4
的最大值为4
(2) •
• =
= cosx-sinx=-
cosx-sinx=-
∴2sin(x- )=
)= ,得sin(x-
,得sin(x- )=
)=
∵ ,得x-
,得x- ∈(-
∈(- ,
, )
)
∴cos(x- )=
)=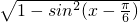 =
=
由此可得cosx=cos[(x- )+
)+ ]=
]=
 -
-
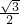 =
=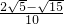
分析:(1)根据向量模的公式,得出 =1且
=1且 =2,再由向量的三角形不等式得
=2,再由向量的三角形不等式得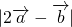 ≤2
≤2 +
+ ,由此不难得到
,由此不难得到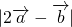 的最大值及相应x的值;
的最大值及相应x的值;
(2)根据向量数量积的运算公式,解出sin(x- )=
)= .再利用配角:x=(x-
.再利用配角:x=(x- )+
)+ ,并结合两角和的余弦公式即可算出cosx的值.
,并结合两角和的余弦公式即可算出cosx的值.
点评:本题以平面向量数量积的运算为载体,着重考查了三角恒等变形、向量的模及其运算性质等知识,属于中档题.
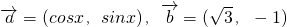
∴
 =
=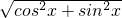 =1,
=1, =
= =2
=2由此可得
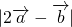 ≤2
≤2 +
+ =4,
=4,当且仅当2
 与
与 共线且反向时,即
共线且反向时,即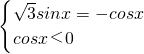 时,等号成立
时,等号成立解之得:x=
 +2kπ,k∈Z
+2kπ,k∈Z综上所述,当x=
 +2kπ(k∈Z)时,
+2kπ(k∈Z)时,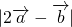 的最大值为4
的最大值为4(2)
 •
• =
= cosx-sinx=-
cosx-sinx=-
∴2sin(x-
 )=
)= ,得sin(x-
,得sin(x- )=
)=
∵
 ,得x-
,得x- ∈(-
∈(- ,
, )
)∴cos(x-
 )=
)=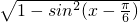 =
=
由此可得cosx=cos[(x-
 )+
)+ ]=
]=
 -
-
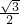 =
=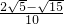
分析:(1)根据向量模的公式,得出
 =1且
=1且 =2,再由向量的三角形不等式得
=2,再由向量的三角形不等式得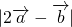 ≤2
≤2 +
+ ,由此不难得到
,由此不难得到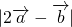 的最大值及相应x的值;
的最大值及相应x的值;(2)根据向量数量积的运算公式,解出sin(x-
 )=
)= .再利用配角:x=(x-
.再利用配角:x=(x- )+
)+ ,并结合两角和的余弦公式即可算出cosx的值.
,并结合两角和的余弦公式即可算出cosx的值.点评:本题以平面向量数量积的运算为载体,着重考查了三角恒等变形、向量的模及其运算性质等知识,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 。
。 的最大值及周期;
的最大值及周期; 满足
满足 ,求
,求 的值.
的值. .
.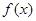 的最大值及取得最大值时的
的最大值及取得最大值时的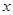 集合;
集合;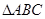 的角
的角 的对边分别为
的对边分别为 ,且
,且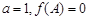 .求
.求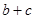 的取值范围
的取值范围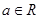 ,
,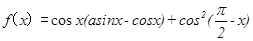 ,满足
,满足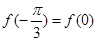 .
.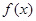 的最大值及此时
的最大值及此时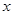 取值的集合;
取值的集合;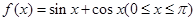
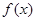 的最大值及
的最大值及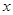 的值;
的值;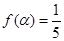 ,求
,求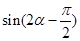 的值.
的值.