题目内容
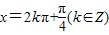是tanx=1成立的（ ）条件．A．充要条件
B．既不充分也不必要条件
C．充分不必要条件
D．必要不充分条件
【答案】分析：根据正切函数的定义，分别判断当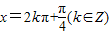
时，tanx=1是否成立及tanx=1时，
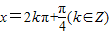是否成立，进而根据充要条件的定义可得答案．
解答：解：当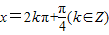
时，tanx=1成立
当tanx=1时，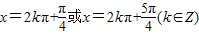
故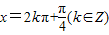
是tanx=1成立的充分不必要条件
故选C
点评：本题考查的知识点是正切函数的定义及充要条件的定义，其中根据正切函数的定义判断出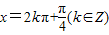
⇒tanx=1与tanx=1⇒
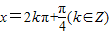的真假是解答的关键．
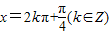时，tanx=1是否成立及tanx=1时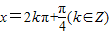，是否成立，进而根据充要条件的定义可得答案．解答：解：当
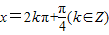时，tanx=1成立当tanx=1时，
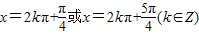
故
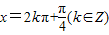是tanx=1成立的充分不必要条件故选C
点评：本题考查的知识点是正切函数的定义及充要条件的定义，其中根据正切函数的定义判断出
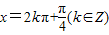⇒tanx=1与tanx=1⇒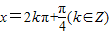的真假是解答的关键． 
练习册系列答案
优学名师名题系列答案
相关题目
“x=2kπ+
(k∈Z)”是“tanx=1”成立的（ ）
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分条件 |
| D、既不充分也不必要条件 |
+
（R∈z）是tanx=1成立的
”是“tanx=1”成立的（ ）