题目内容
(本小题满分14分)
在数列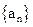 中,
中,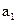 =0,且对任意k
=0,且对任意k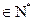 ,
,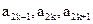 成等差数列,其公差为2k.
成等差数列,其公差为2k.
(Ⅰ)证明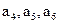 成等比数列;
成等比数列;
(Ⅱ) 求数列
求数列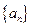 的通项公
的通项公 式;
式;
(Ⅲ)记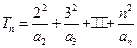 ,证明
,证明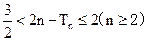 .
.
在数列
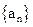 中,
中,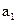 =0,且对任意k
=0,且对任意k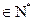 ,
,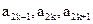 成等差数列,其公差为2k.
成等差数列,其公差为2k.(Ⅰ)证明
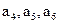 成等比数列;
成等比数列;(Ⅱ)
 求数列
求数列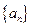 的通项公
的通项公 式;
式;(Ⅲ)记
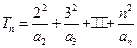 ,证明
,证明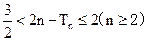 .
.(Ⅰ)见解析(Ⅱ) (Ⅲ)见解析
(Ⅲ)见解析
 (Ⅲ)见解析
(Ⅲ)见解析(本小题主要考查等差数列的定义及前n项和公式、等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法,满分14分。
(I)证明:由题设可知, ,
, ,
, ,
, ,
,
 。
。
从而 ,所以
,所以 ,
, ,
, 成等比数列。
成等比数列。
(II)解:由题设可得
所以

 .
.
由 ,得
,得 ,从而
,从而 .
.
所以数列 的通项公式为
的通项公式为 或写为
或写为 ,
, 。
。
(III)证明:由(II)可知 ,
, ,
,
以下分两种情况进行讨论:
(1) 当n为偶数时,设n=2m
若 ,则
,则 ,
,
若 ,则
,则


 .
.
所以 ,从而
,从而
(2) 当n为奇数时,设 。
。


所以 ,从而
,从而
综合(1)和(2)可知,对任意 有
有
(I)证明:由题设可知,
 ,
, ,
, ,
, ,
, 。
。从而
 ,所以
,所以 ,
, ,
, 成等比数列。
成等比数列。(II)解:由题设可得

所以


 .
.由
 ,得
,得 ,从而
,从而 .
.所以数列
 的通项公式为
的通项公式为 或写为
或写为 ,
, 。
。(III)证明:由(II)可知
 ,
, ,
,以下分两种情况进行讨论:
(1) 当n为偶数时,设n=2m

若
 ,则
,则 ,
,若
 ,则
,则

 .
.所以
 ,从而
,从而
(2) 当n为奇数时,设
 。
。

所以
 ,从而
,从而
综合(1)和(2)可知,对任意
 有
有

练习册系列答案
相关题目
 满足
满足 ,
,
 ,求数列
,求数列 的前n项和
的前n项和 .
. 满足:
满足: ,
, ,
, .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.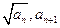 )(n
)(n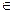 N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;
N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;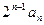 (n∈N*),求数列{bn}的前n项和
(n∈N*),求数列{bn}的前n项和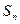 。
。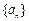 的前n项和
的前n项和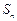 满足:
满足: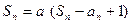 (
(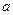 为常数,
为常数,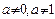 )(Ⅰ)求
)(Ⅰ)求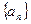 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设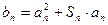 ,若数列
,若数列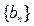 为等比数列,求
为等比数列,求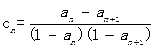 ,数列
,数列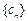 的前n项和为
的前n项和为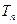 . 求证:
. 求证: 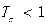 .
. ,并且这三个数分别加上
,并且这三个数分别加上 ,
, ,
, 后就成了等比数列,求这三个数排成的等差数列.
后就成了等比数列,求这三个数排成的等差数列.
 )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 求和:
求和: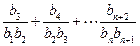
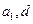 为实数,首项为
为实数,首项为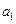 ,公差为
,公差为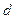 的等差数列
的等差数列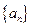 的前
的前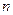 项和为
项和为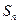 ,满足
,满足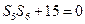 ,
,