题目内容
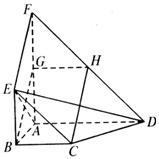
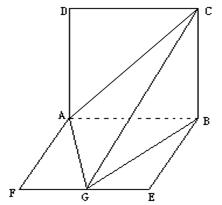
如图,平面ABEF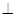 ABCD,四边形ABEF与ABCD都是直角梯形,
ABCD,四边形ABEF与ABCD都是直角梯形,


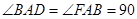 °,BC
°,BC  AD,BE
AD,BE  FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明四边形BCHG是平行四边行.
(2)C、D、E、F四点是否共面?为什么?
(3)设AB=BE,证明平面ADE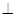 平面CDE.
平面CDE.
【答案】
(1)证明:由题设知,FG=GA,FH=HD,所以GH 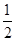 AD.
AD.
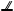
 又BC
又BC 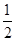 AD,故GH BC.
AD,故GH BC.
 所以四边形BCHG是平行四边形.
所以四边形BCHG是平行四边形.
(2)C、D、F、E四点共面.理由如下:

 由BE
由BE 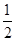 AF,G是FA的中点知,BE GF,所以EF//BG .
AF,G是FA的中点知,BE GF,所以EF//BG .
由(1)知BG//CH,所以EF//CH,故EC、FH共面.
又点D在直线FH上,
所以C、D、F、E四点共面.
(3)证明:连结EG.由AB=BE,BE
AG及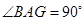 知ABEG是正方形,
知ABEG是正方形,
故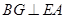 .由题设知,FA、AD、AB两两垂直,故AD
.由题设知,FA、AD、AB两两垂直,故AD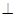 平面FABE,
平面FABE,
因此EA是ED在平面FABE内的射影.根据三垂线定理,BG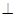 ED.
ED.
又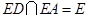 ,所以
,所以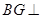 平面ADE.
平面ADE.
由(1)知, CH//BG,所以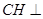 平面ADE.
平面ADE.
由(2)知 平面CDE,故
平面CDE,故 平面CDE,得平面ADE
平面CDE,得平面ADE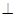 平面CDE.
平面CDE.
【解析】略

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC= 如图平面四边形ABCD中,AB=AD=a,BC=CD=BD 设∠BAD=θ
如图平面四边形ABCD中,AB=AD=a,BC=CD=BD 设∠BAD=θ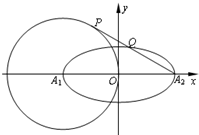 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆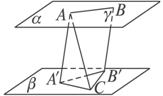
 (本题满分12分).如图:平面
(本题满分12分).如图:平面