Question

如图,平面α∥平面β,A、B∈α,C∈β,AA′⊥β于A′,BB′⊥β于B′,若AC⊥AB,AC与β成60°的角,AC=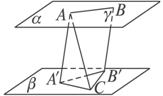8 cm,B′C=6 cm,求异面直线AC与BB′间的距离.

Answer 1

解析:∵AA′⊥β于A′,BB′⊥β于B′,

且A′B′?β,∴AA′∥BB′,AA′⊥A′B′.

∴AA′和BB′可确定一平面,设为γ,且γ∩α=ΑΒ,γ∩β=A′B′.

∵α∥β,∴AB∥A′B′.

又∵AB⊥AC,

∴A′B′⊥AC.

又∵AA′⊥β,

∴A′B′⊥A′C.

由AA′⊥A′B′,AA′∩A′C=A′,

∴A′B′⊥平面A′AC.

由AA′∥BB′,∴BB′∥平面AA′C.

∴BB′与AC间的距离为BB′与平面AA′C间的距离.由A′B′⊥平面A′AC,

∴BB′与AC间的距离为A′B′的长.

由AA′⊥β,AC=8cm,

∴∠ACA′=60°.

∴A′C=4cm.

又∵B′C=6cm,

∴A′B′=cm,

即异面直线AC和BB′间的距离为cm.