Question

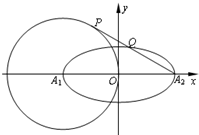如图平面直角坐标系xOy中，椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率e=

3

2

，A₁，A₂分别是椭圆的左、右两个顶点，圆A₁的半径为a，过点A₂作圆A₁的切线，切点为P，在x轴的上方交椭圆于点Q．则

PQ

QA2

=

 

．

Answer 1

分析：连结A₂P，可得△OPA₂是边长为a的正三角形，由此算出PA₁、PO的方程，联解求出点P的横坐标m=-

1

2

a．由A₂P与圆A₁相切得到A₂P⊥PA₁，从而得到直线A₂P的方程，由椭圆的离心率化简椭圆方程，并将PA₂的方程与椭圆方程联解算出Q点横坐标s=

a

7

．由

PQ

QA2

=

xQ-xP

xA2-xQ

，把前面算出的横坐标代入即可求得

PQ

QA2

的值．

解答：解：连结PO、PA₁，可得△POA₁是边长为a的等边三角形，
∴∠PA₁O=∠POA₁=60°，可得直线PA₁的斜率k₁=tan60°=

3

，
直线PO的斜率k₂=tan120°=-

3

，
因此直线PA₁的方程为y=

3

（x+a），直线PO的方程为y=-

3

x，
设P（m，n），联解PO、PA₁的方程可得m=-

1

2

a．
∵圆A₁与直线PA₂相切于P点，
∴PA₂⊥PA₁，可得∠PA₂O=90°-∠PA₁O=30°，
直线PA₂的斜率k=tan150°=-

3

3

，因此直线PA₂的方程为y=-

3

3

（x-a），
∵椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率e=

3

2

，∴

c

a

=

a2-b2 a2

=

3

2

，解之得a²=4b²，
由

x2 a2 + 4y2 a2 =1 y=- 3 3 (x-a)

消去y，得

7

3

x2-

8

3

ax+

1

3

a2=0，解之得x=a或x=

a

7

．
∵直线PA₂交椭圆于A₂（a，0）与Q点，∴设Q（s，t），可得s=

a

7

．
由此可得

PQ

QA2

=

xQ-xP

xA2-xQ

=

s-m

a-s

=

a 7 + 1 2 a

a- a 7

=

3

4

．
故答案为：

3

4

点评：本题给出与椭圆相关的直线与圆相切的问题，求线段的比值．着重考查了直线的基本量与基本形式、直线与圆的位置关系、椭圆的标准方程与简单几何性质等知识，属于中档题．