题目内容
 易知n2=1+2+3+…+n+(n-1)+…+2+1,故有13=1,23=2•22=2(1+2+1)=2+4+2;33=3•32=3(1+2+3+2+1)=3+6+9+6+3,…,这些通过分拆得到的数可组成数阵认真观察数阵,可以求出和式S=13+23+33+…+203的值为
易知n2=1+2+3+…+n+(n-1)+…+2+1,故有13=1,23=2•22=2(1+2+1)=2+4+2;33=3•32=3(1+2+3+2+1)=3+6+9+6+3,…,这些通过分拆得到的数可组成数阵认真观察数阵,可以求出和式S=13+23+33+…+203的值为考点:数列的求和,归纳推理
专题:等差数列与等比数列
分析:由于n3=n(1+2+3+…+n-1+n+n-1+…+2+1),结合数阵可得:S=13+23+33+…+203=(1+2+…+20)(1+2+…+20),即可得出.
解答:
解:n3=n(1+2+3+…+n-1+n+n-1+…+2+1),
结合数阵可得:
∴S=13+23+33+…+203=(1+2+…+20)(1+2+…+20)
=
×
=44100.
故答案为:44100.
结合数阵可得:
∴S=13+23+33+…+203=(1+2+…+20)(1+2+…+20)
=
| 20×21 |
| 2 |
| 20×21 |
| 2 |
故答案为:44100.
点评:本题考查了观察分析猜想归纳求数列的通项公式的方法,考查了等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
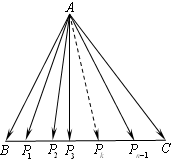 若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量
若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列关于频率与概率的关系表示正确的是( )
| A、频率就是概率 |
| B、频率是客观存在的,与试验次数无关 |
| C、概率是随机的,在实验前不能确定 |
| D、随着试验次数的增加,频率一般会越来越接近概率 |
设m、n是空间两条不同的直线,α、β、γ是三个不同的平面,则下列命题是真命题的是( )
| A、如果α⊥γ,β⊥γ,则α∥β | ||
| B、如果α⊥β,m∥α,则m⊥β | ||
C、如果m∥n,n
| ||
| D、如果m⊥α,n⊥α,则m∥n |
已知向量
、
,|
|=4,|
|=3,
与
的夹角等于60°,则(
+2
)•(
-
)等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-4 | B、4 | C、-2 | D、2 |
下列函数中既是偶函数又在(-∞,0)上是减函数的是( )
| A、f(x)=x4 | ||
| B、f(x)=x5 | ||
C、f(x)=
| ||
D、f(x)=
|