题目内容
已知函数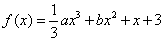 ,其中
,其中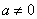
(1)当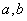 满足什么条件时,
满足什么条件时,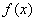 取得极值
取得极值 ?
?
(2)已知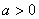 ,且
,且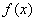 在区间
在区间 上单调递增,试用
上单调递增,试用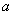 表示出
表示出 的取值范围.
的取值范围.
解析 (1)依题可设 (
( ),则
),则 ;
;
又 的图像与直线
的图像与直线 平行
平行 

 ,
,  ,
,
设 ,则
,则



当且仅当 时,
时, 取得最小值,即
取得最小值,即 取得最小值
取得最小值
当 时,
时, 解得
解得

当 时,
时, 解得
解得
(2)由 (
( ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时
时 ,方程
,方程 有二解
有二解 ,
,
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即
 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
( ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,点
中,点 .则以线段
.则以线段
 为邻边的平行四边形两条对角线的长分别为 .
为邻边的平行四边形两条对角线的长分别为 . ,各项均为正整数的等差数列中,若
,各项均为正整数的等差数列中,若 ,
,  , 则
, 则 的最小值等于____.
的最小值等于____.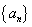 和
和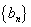 满足
满足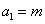 ,
, 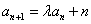 ,
, 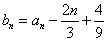 .
.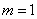 时,求证: 对于任意的实数
时,求证: 对于任意的实数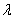 ,
,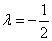 时,试判断
时,试判断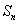 为数列
为数列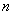 项和,在(Ⅱ)的条件下,是否存在实数
项和,在(Ⅱ)的条件下,是否存在实数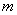 ,使得对任意的正整数
,使得对任意的正整数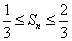 ?若存在,请求出
?若存在,请求出 中,点P在曲线
中,点P在曲线
 上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 .解析
上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 .解析  在两个极值点
在两个极值点 ,且
,且
 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;
 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 等于 ( )
等于 ( ) 或
或 B.
B. C.
C. 或
或
 ,
, ,
, ,则
,则 .
. 为正方体的两个顶点,
为正方体的两个顶点, 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出 平面
平面 的图形的序号是( )
的图形的序号是( )