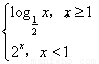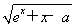题目内容
求下列函数的值域:
(1) f(x)= ;
;
(2) g(x)= ;
;
(3) y=log3x+logx3-1.
(1) (2)
(2)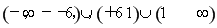
(3)(-∞,-3]∪[1,+∞).
【解析】(1)由 解得-3≤x≤1.
解得-3≤x≤1.
∴ f =
=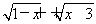 的定义域是
的定义域是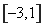 .∵ y≥0,∴ y2=4+2
.∵ y≥0,∴ y2=4+2 ,
,
即y2=4+2 .令t
.令t =-
=- +4
+4 .
.
∵ x∈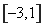 ,由t
,由t =0,t
=0,t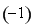 =4,t
=4,t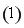 =0,
=0,
∴ 0≤t≤4,从而y2∈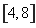 ,即y∈
,即y∈ ,∴ 函数f
,∴ 函数f 的值域是
的值域是 .
.
(2) g =
= .
.
∵ x≠3且x≠4,∴ g ≠1且g
≠1且g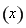 ≠-6.
≠-6.
∴ 函数g 的值域是
的值域是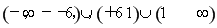 .
.
(3) 函数的定义域为{x|x>0且x≠1}.
当x>1时,log3x>0,y=log3x+logx3-1≥2  -1=1;
-1=1;
当0<x<1时,log3x<0,y=log3x+logx3-1=-[(-log3x)+(-logx3)]≤-2-1=-3.
所以函数的值域是(-∞,-3]∪[1,+∞).

练习册系列答案
相关题目