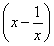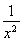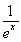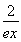Question

设函数f(x)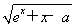＝ (a∈R，e为自然对数的底数)．若存在b∈[0，1]使f(f(b))＝b成立，则a的取值范围是________．

 

Answer 1

[1，e]

【解析】若存在b∈[0，1]使f(f(b))＝b成立，

则A(b，f(b))，A′(f(b)，b)都在y＝f(x)的图象上．

又f(x)＝在[0，1]上单调递增，

所以(xA′－xA)(yA′－yA)≥0，

即(f(b)－b)(b－f(b))≥0，所以(f(b)－b)2≤0，

所以f(b)＝b，从而f(x)＝x在[0，1]上有解，

即＝x在[0，1]上有解，

所以a＝ex＋x－x2，x∈[0，1]，

令φ(x)＝ex＋x－x2，x∈[0，1]，

则φ′(x)＝ex－2x＋1≥0，

所以φ(x)在[0，1]上单调递增．

又φ(0)＝1，φ(1)＝e，

所以φ(x)∈[1，e]，即a∈[1，e]．