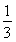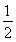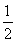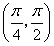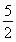题目内容
已知函数f(x)=lnx- (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.
-3e
【解析】f′(x)= +
+ =
= ,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1-
,令f′(x)=0,则x=-m,且当x<-m时,f′(x)<0,f(x)单调递减,当x>-m时,f′(x)>0,f(x)单调递增.若-m≤1,即m≥-1时,f(x)min=f(1)=-m≤1,不可能等于4;若1<-m≤e,即-e≤m<-1时,f(x)min=f(-m)=ln(-m)+1,令ln(-m)+1=4,得m=-e3?(-e,-1);若-m>e,即m<-e时,f(x)min=f(e)=1- ,令1-
,令1- =4,得m=-3e,符合题意.综上所述,m=-3e.
=4,得m=-3e,符合题意.综上所述,m=-3e.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目