题目内容
(1)求证:(2)已知sin2Acsc2B+cos2Acos2C=1(cosA≠0),求证:sin2C=tan2Acot2B.
证明:(1)右边=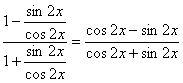
=![]()
=左边.
(2)∵sin2Acsc2B+cos2A(1-sin2C)=1,∴cos2Asin2C=sin2Acsc2B-(1-cos2A).
∴sin2C=![]() (csc2B-1)=tan2A·cot2B.
(csc2B-1)=tan2A·cot2B.

练习册系列答案
相关题目
题目内容
(1)求证:(2)已知sin2Acsc2B+cos2Acos2C=1(cosA≠0),求证:sin2C=tan2Acot2B.
证明:(1)右边=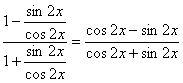
=![]()
=左边.
(2)∵sin2Acsc2B+cos2A(1-sin2C)=1,∴cos2Asin2C=sin2Acsc2B-(1-cos2A).
∴sin2C=![]() (csc2B-1)=tan2A·cot2B.
(csc2B-1)=tan2A·cot2B.
