题目内容
设向量a=(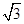 sin x,sin x),b="(cos" x,sin x),x∈
sin x,sin x),b="(cos" x,sin x),x∈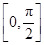 .
.
(1)若|a|=|b|,求x的值;
(2)设函数f(x)=a·b,求f(x)的最大值.
(1) x=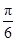 (2)
(2) 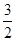
解析解:(1)由|a|=|b|得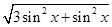 =
=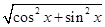 ,
,
即4sin2x=1.
又因为sin2x+cos2x=1,x∈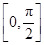 .
.
所以sin x=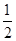 ,x=
,x=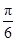 .
.
(2)f(x)=a·b=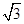 sin xcos x+sin 2x,x∈
sin xcos x+sin 2x,x∈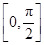 .
.
f(x)= sin 2x+
sin 2x+ =
= sin 2x-
sin 2x-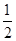 cos 2x+
cos 2x+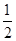 =sin(2x-
=sin(2x-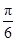 )+
)+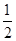 .
.
又2x-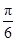 ∈
∈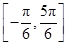 ,f(x)∈
,f(x)∈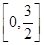 .
.
即f(x)最大值为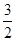 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知数列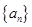 中,
中,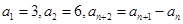 ,则
,则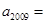 ( )
( )
| A.6 | B.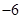 | C.3 | D.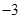 |
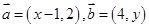 ,若
,若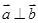 ,则
,则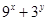 的最小值为 .
的最小值为 .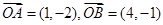 ,
,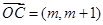 .
. 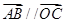 ,求实数
,求实数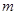 的值;
的值; 为直角三角形,求实数
为直角三角形,求实数 ,
,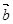 ,
,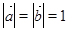 ,且
,且 ,其中
,其中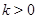
 ,求
,求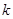 的值;
的值;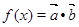 ,是否存在实数
,是否存在实数 ,使得
,使得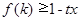 对任意的
对任意的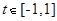 恒成立?若存在,求出实数
恒成立?若存在,求出实数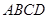 中,
中,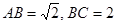 ,点
,点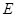 是
是 边的中点,点
边的中点,点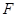 在边
在边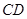 上.
上. 是对角线
是对角线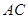 的中点,
的中点, 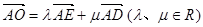 ,求
,求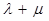 的值;
的值;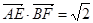 ,求线段
,求线段 的长.
的长.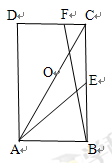
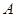 、
、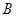 、
、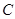 在一条直线上,
在一条直线上,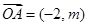 ,
,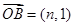 ,
,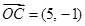 ,且
,且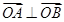 ,其中
,其中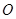 为坐标原点.
为坐标原点.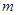 ,
,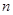 的值;
的值;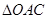 的重心为
的重心为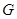 ,若存在实数
,若存在实数 ,使
,使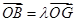 ,试求
,试求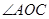 的大小.
的大小. =λ
=λ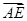 ,
,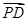 =μ
=μ ,
, =a,
=a, =b.
=b.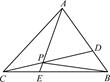
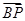 ;
; 的三内角
的三内角 、
、 、
、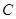 所对的边分别是
所对的边分别是 ,
,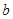 ,
,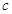 ,向量
,向量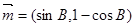 与向量
与向量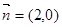 的夹角
的夹角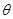 的余弦值为
的余弦值为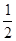
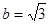 ,求
,求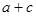 的范围。
的范围。