题目内容
已知 ,
,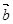 ,
,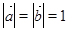 ,且
,且 ,其中
,其中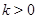
(1)若 与
与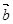 的夹角为
的夹角为 ,求
,求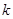 的值;
的值;
(2)记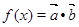 ,是否存在实数
,是否存在实数 ,使得
,使得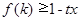 对任意的
对任意的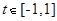 恒成立?若存在,求出实数
恒成立?若存在,求出实数 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
(1)1;(2)不存在
解析试题分析:(1)先运用向量的数量积公式求出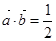 ,对式子
,对式子 两边平方以及结合
两边平方以及结合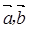 的模均是1得到关于
的模均是1得到关于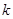 的等式
的等式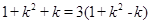 ;(2)利用(1)中
;(2)利用(1)中 平方求出的式子将
平方求出的式子将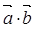 表示成关于
表示成关于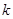 的式子
的式子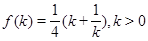 ,均值不等式求得
,均值不等式求得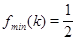 ,再利用
,再利用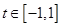 解得
解得 .
.
(1)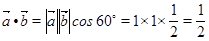 ,由
,由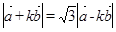 ,
,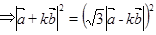
得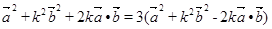 ,即
,即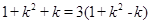
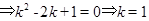 (6分)
(6分)
由(1)得,
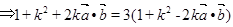 ,即可得,
,即可得,
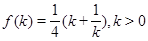 ,因为
,因为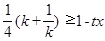 对于任意
对于任意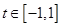 恒成立,又因为
恒成立,又因为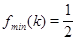 ,所以
,所以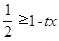 ,即
,即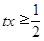 对于任意
对于任意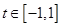 恒成立,构造函数
恒成立,构造函数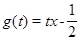
从而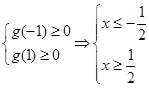 由此可知不存在实数
由此可知不存在实数 使之成立.
使之成立.
考点:1、向量的计算;(2)存在性问题.

练习册系列答案
相关题目
设函数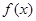 )定义为如下数表,且对任意自然数n均有xn+1=
)定义为如下数表,且对任意自然数n均有xn+1=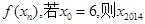 的值为( )
的值为( )
| A.1 | B.2 | C.4 | D.5 |
 ,
, ,
, ,且
,且 、
、 、
、 三点共线,
三点共线, 时,若
时,若 为直线的斜率,则过点
为直线的斜率,则过点 的直线方程为 ;
的直线方程为 ; 时,若等差数列
时,若等差数列 前9项的和等于前4项的和,
前9项的和等于前4项的和, ,则
,则 .
. =
= +t
+t ,试问:
,试问: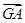 +
+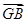 +
+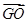 ;
; =a,
=a, =b,
=b, =ma,
=ma,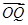 =nb,求证:
=nb,求证: +
+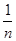 =3.
=3.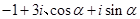 (
(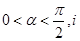 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为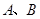 ,点
,点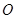 是坐标原点.
是坐标原点.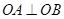 ,求
,求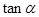 的值;
的值; 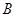 点的横坐标为
点的横坐标为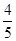 ,求
,求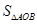 .
. 中,角
中,角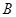 为锐角,已知内角
为锐角,已知内角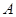 、
、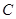 所对的边分别为
所对的边分别为 、
、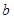 、
、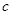 ,向量
,向量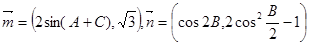 且向量
且向量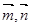 共线.
共线.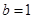 ,且
,且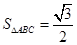 ,求
,求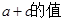 .
.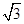 sin x,sin x),b="(cos" x,sin x),x∈
sin x,sin x),b="(cos" x,sin x),x∈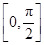 .
.