题目内容
已知平面直角坐标系内三点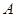 、
、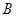 、
、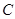 在一条直线上,
在一条直线上,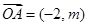 ,
,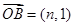 ,
,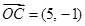 ,且
,且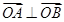 ,其中
,其中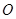 为坐标原点.
为坐标原点.
(1)求实数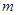 ,
,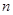 的值;
的值;
(2)设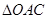 的重心为
的重心为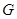 ,若存在实数
,若存在实数 ,使
,使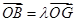 ,试求
,试求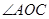 的大小.
的大小.
(1) 或
或 ,(2)
,(2)
解析试题分析:(1)由A,B,C三点共线,得 与
与 共线,又
共线,又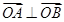 ,可得关于
,可得关于 方程组,解得
方程组,解得 的值;(2)由
的值;(2)由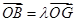 ,得
,得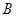 为
为 的中点,再利用
的中点,再利用 即可求解.
即可求解.
试题解析:
(1)由于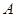 、
、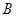 、
、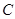 三点在一条直线上,则
三点在一条直线上,则 ∥
∥ ,
,
而 ,
,
∴ ,
,
又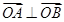 ∴
∴ ,联立方程组解得
,联立方程组解得 或
或 . (6分)
. (6分)
(2)若存在实数 ,使
,使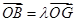 ,则
,则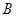 为
为 的中点,故
的中点,故 .
.
∴ ,
,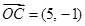
∴ ,∴
,∴ (12分)
(12分)
考点:向量平行,垂直的充要条件的坐标形式,向量的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列 对任意的
对任意的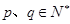 满足
满足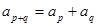 且
且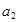 =6,那么
=6,那么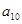 等于( )
等于( )
| A.165 | B.33 | C.30 | D.21 |
 的模为1,且
的模为1,且 满足
满足 ,则
,则 在
在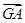 +
+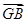 +
+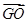 ;
; =a,
=a, =b,
=b, =ma,
=ma,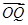 =nb,求证:
=nb,求证: +
+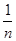 =3.
=3. 中,角
中,角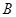 为锐角,已知内角
为锐角,已知内角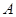 、
、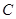 所对的边分别为
所对的边分别为 、
、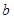 、
、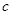 ,向量
,向量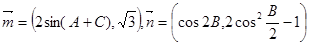 且向量
且向量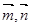 共线.
共线.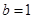 ,且
,且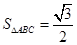 ,求
,求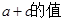 .
.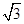 sin x,sin x),b="(cos" x,sin x),x∈
sin x,sin x),b="(cos" x,sin x),x∈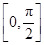 .
. ,
,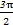 ).
). |=|
|=|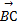 |,求角α的值.
|,求角α的值.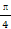 )的值.
)的值.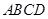 中,
中,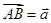 ,
,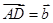 ,
,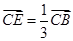 ,
,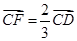 。
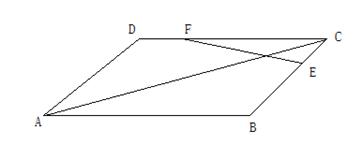
。
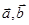 表示
表示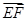 ;
;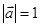 ,
,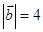 ,
,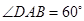 ,分别求
,分别求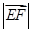 和
和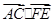 的值。
的值。