题目内容
设函数 .
.
(Ⅰ) 若函数 在
在 上为增函数, 求实数
上为增函数, 求实数 的取值范围;
的取值范围;
(Ⅱ) 求证:当 且
且 时,
时, .
.
(Ⅰ) 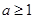 ;(Ⅱ)参考解析
;(Ⅱ)参考解析
解析试题分析:(Ⅰ)首先考虑函数的定义域.通过对函数求导可得 函数的单调区间.因为要求函数 在
在 上为增函数,所以可得结论.本小题的是含参数的函数问题.
上为增函数,所以可得结论.本小题的是含参数的函数问题.
(Ⅱ)由于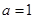 可得函数
可得函数 在
在 上为增函数.又因为f(1)=0.所以
上为增函数.又因为f(1)=0.所以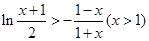 .通过对x,n的值的赋值即.
.通过对x,n的值的赋值即. .则
.则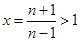 ,
, .即可得结论.最后的构造是本题的关键.要根据所要证得结论结合数列的思想.
.即可得结论.最后的构造是本题的关键.要根据所要证得结论结合数列的思想.
试题解析: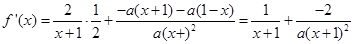
= .所以在
.所以在 上为减函数.在
上为减函数.在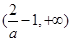 上为增函数.所以在
上为增函数.所以在 处取得极小值.
处取得极小值.
(Ⅰ)依题意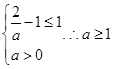 .
.
(Ⅱ)由(Ⅰ)知.当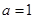 时.
时.  在
在 上为增函数.当x>1时有f(x)>f(1)=0.即
上为增函数.当x>1时有f(x)>f(1)=0.即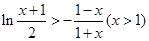 .取
.取 .则
.则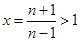 ,
, .即有
.即有 .所以
.所以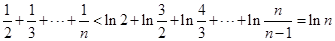 .
.
考点:1.含参数的函数问题.2.函数的单调性问题.3.函数、不等式、数列相结合的题型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,其中
,其中 为常数
为常数 为奇函数,试确定
为奇函数,试确定 恒成立,求实数
恒成立,求实数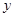 (单位:微克)与时间
(单位:微克)与时间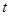 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.
 ;
; 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: ).
). 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. .
.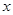 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当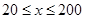 时,车流速度
时,车流速度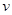 是车流密度x的一次函数.
是车流密度x的一次函数.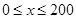 时,求函数
时,求函数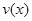 的表达式;
的表达式;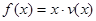 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时) .
. 时,指出
时,指出 的单调递减区间和奇偶性(不需说明理由);
的单调递减区间和奇偶性(不需说明理由); 的零点;
的零点; 不等式
不等式 恒成立,求实数
恒成立,求实数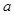 的取值范围。
的取值范围。 在区间
在区间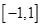 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程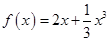 的两个非零实根为
的两个非零实根为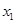 、
、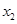 .试问:是否存在实数
.试问:是否存在实数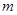 ,使得不等式
,使得不等式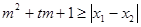 对任意
对任意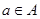 及
及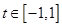 恒成立?若存在,求
恒成立?若存在,求
 ,判断函数
,判断函数 在
在 上的单调性并用定义证明;
上的单调性并用定义证明; 的取值范围.
的取值范围.