题目内容
(本小题满分12分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量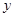 (单位:微克)与时间
(单位:微克)与时间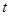 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.
(Ⅰ)写出第一次服药后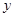 与
与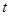 之间的函数关系式
之间的函数关系式 ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: ).
).
(Ⅰ) (Ⅱ)服药
(Ⅱ)服药 小时(即
小时(即 分钟)开始有治疗效果,治疗效果能持续
分钟)开始有治疗效果,治疗效果能持续 小时
小时
解析试题分析:(Ⅰ)第一段图像是一条过原点的直线,可以用线段两端点的坐标求其斜率,第二段图像解析式已给出,在最后作答时注意写成分段函数。(Ⅱ)在两端函数上分别求 的值,因为此函数在第一段上是增函数,在第二段上是减函数,所以在第一段中求得的
的值,因为此函数在第一段上是增函数,在第二段上是减函数,所以在第一段中求得的 就是开始有治疗效果的时间,在第二段函数中求得的
就是开始有治疗效果的时间,在第二段函数中求得的 就是即将失去治疗效果的时间。
就是即将失去治疗效果的时间。 即为治疗效果能持续的时间。
即为治疗效果能持续的时间。
试题解析:(Ⅰ)根据图象知:当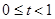 时,
时, ;
; 
当 时,
时, ,由
,由 时,
时, 得
得
所以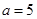 ,即
,即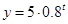

因此
(Ⅱ)根据题意知:
当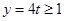 时,
时, ;
; 
当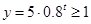 时,
时,
所以

所以 ,
,
因此服药 小时(即
小时(即 分钟)开始有治疗效果,治疗效果能持续
分钟)开始有治疗效果,治疗效果能持续 小时.
小时. 
考点:函数解析式的求法,

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量,并求
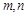 的值.
的值.  (其中
(其中 且
且 ),
), 是
是 的反函数.
的反函数. 的方程
的方程 在区间
在区间 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围; 时,讨论函数
时,讨论函数 ,其中
,其中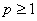 .记
.记 ,数列
,数列 的前
的前 项的和为
项的和为 (
( ),
), .
. (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件.
 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数 ,求
,求 的值。
的值。 在[
在[ ,+∞)上的单调性.
,+∞)上的单调性.
 .
. 在
在 上为增函数, 求实数
上为增函数, 求实数 的取值范围;
的取值范围; 且
且 时,
时, .
.  是实数,
是实数,
 成立;
成立; 均为增函数
均为增函数