题目内容
给出函数 .
.
求函数的定义域;
判断函数的奇偶性;
(1) ;(2)奇函数
;(2)奇函数
解析试题分析:(1)由对数函数的定义域是真数大于零,所以可得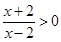 .分式不等式转化为二次不等式即(x+2)(x-2)>0.所以求得x的范围.
.分式不等式转化为二次不等式即(x+2)(x-2)>0.所以求得x的范围.
(2)函数 的奇偶性的判断,通过奇偶性的定义来判断.因为
的奇偶性的判断,通过奇偶性的定义来判断.因为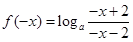 =
=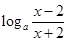 .通过对数的性质可得f(-x)=
.通过对数的性质可得f(-x)=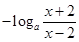 =
=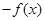 .所以可得函数
.所以可得函数 是奇函数的.
是奇函数的.
试题解析:( 1)由题意,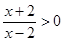 解得:
解得: ,所以,函数定义域为
,所以,函数定义域为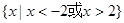 .
.
(2)由(1)可知定义域关于原点对称,则 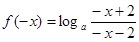 =
=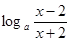 =
=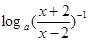 =
=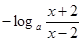 =
=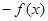 .所以函数
.所以函数 为奇函数.
为奇函数.
考点:1.对数函数的知识.2.对数函数的定义域.3.函数的奇偶性.

练习册系列答案
相关题目

 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数 ,求
,求 的值。
的值。
 .
.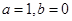 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数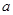 的取值范围.
的取值范围. .
. 在
在 上为增函数, 求实数
上为增函数, 求实数 的取值范围;
的取值范围; 且
且 时,
时, .
.  ,两个函数
,两个函数 ,
,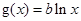 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
.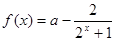 ,
,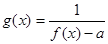 若函数
若函数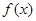 为奇函数,求
为奇函数,求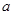 的值.
的值.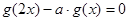 ,有唯一实数解,求
,有唯一实数解,求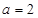 ,则是否存在实数
,则是否存在实数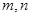
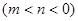 ,使得函数
,使得函数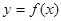 的定义域和值域都为
的定义域和值域都为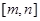 。若存在,求出
。若存在,求出 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
 ;
; 时, 对
时, 对 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围.