题目内容
设 ,其中
,其中 为常数
为常数
(1) 为奇函数,试确定
为奇函数,试确定 的值
的值
(2)若不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(1) ;(2)
;(2) .
.
解析试题分析:(1)因为 为奇函数且
为奇函数且 ,
, 得
得 ;(2)不等式
;(2)不等式 恒成立等价于
恒成立等价于 .
.
试题解析:(1)由 得
得 ;
;
(2) ,因为
,因为 ,所以
,所以 ,因为
,因为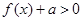 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 即
即 .
.
考点:本题考查奇函数的性质,当 ,
, ;不等式恒成立的问题.
;不等式恒成立的问题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量,并求
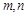 的值.
的值.  在区间[1,+∞)上是减函数.
在区间[1,+∞)上是减函数. (其中
(其中 且
且 ),
), 是
是 的反函数.
的反函数. 的方程
的方程 在区间
在区间 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围; 时,讨论函数
时,讨论函数 ,其中
,其中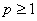 .记
.记 ,数列
,数列 的前
的前 项的和为
项的和为 (
( ),
), .
. 的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
. 的值;
的值; 为增函数;
为增函数; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围. 对任意实数
对任意实数 均有
均有 ,且当
,且当 时,
时,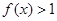 .
.
 时,解不等式
时,解不等式
 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件. .
. 在
在 上为增函数, 求实数
上为增函数, 求实数 的取值范围;
的取值范围; 且
且 时,
时, .
.