题目内容
设数列{an}的前n项和为Sn,且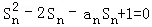 ,n=1,2,3
,n=1,2,3
(1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{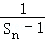 }是等差数列;
}是等差数列;
(3)求S1•S2•S3 S2011•S2012的值.
(1) ,
,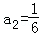 ;(2)SnSn﹣1﹣2Sn+1=0;(3)
;(2)SnSn﹣1﹣2Sn+1=0;(3)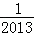 .
.
解析试题分析:(1)直接利用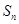 与
与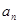 的关系式求
的关系式求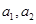 的值;(2)当
的值;(2)当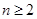 时,把
时,把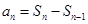 代入已知关系式可得与
代入已知关系式可得与 的关系式,再由此关系式,去凑出
的关系式,再由此关系式,去凑出 和
和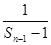 ,可得所求数列
,可得所求数列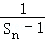 是等差数列,进而得通项
是等差数列,进而得通项 的表达式,从而得
的表达式,从而得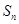 的表达式;(3)由(2)中
的表达式;(3)由(2)中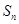 的表达式易求S1•S2•S3 S2011•S2012的值.
的表达式易求S1•S2•S3 S2011•S2012的值.
试题解析:(1)解:当n=1时,由已知得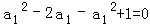 ,解得
,解得 ,
,
同理,可解得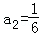 . (4分)
. (4分)
(2)证明:由题设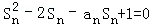 ,
,
当n≥2时,an=Sn﹣Sn﹣1,代入上式,得SnSn﹣1﹣2Sn+1=0,
∴ , (7分)
, (7分)
∴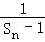 =﹣1+
=﹣1+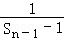 ,
,
∴{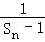 }是首项为
}是首项为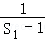 =﹣2,公差为﹣1的等差数列, (10分)
=﹣2,公差为﹣1的等差数列, (10分)
∴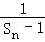 =﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=
=﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=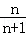 . (12分)
. (12分)
(3)解:S1•S2•S3 S2011•S2012= •
•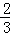 •
•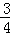 •
•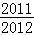 •
•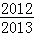 =
=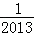 . (14分)
. (14分)
考点:1、等差数列;2、数列的前n项和与通项的综合应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 满足:①对任意
满足:①对任意 ,
,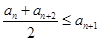 ;②存在常数
;②存在常数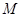 ,对任意
,对任意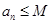 ,则称数列
,则称数列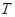 数列”.
数列”.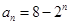
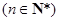 ,证明:数列
,证明:数列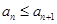 ;
;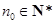 ,数列
,数列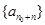 为等差数列.
为等差数列.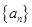 的通项公式为
的通项公式为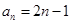 ,数列
,数列 的前
的前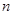 项和为
项和为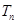 ,且满足
,且满足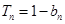 .
.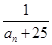 是
是 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列, ,求数列{bm}的前m项和Tm.
,求数列{bm}的前m项和Tm. 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,记
,记 .
.  ,
, 的值;
的值; 的通项公式;
的通项公式; 求证:对任意
求证:对任意 .
. 的各项均为正数,
的各项均为正数,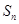 为其前
为其前 项和,对于任意的
项和,对于任意的 ,总有
,总有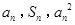 成等差数列.
成等差数列.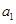 ;
;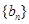 的前
的前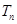 ,且
,且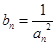 ,求证:对任意正整数
,求证:对任意正整数
 的前
的前 项和为
项和为 ,且
,且 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前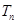 ,证明:
,证明: .
. 中,已知
中,已知 ,公比
,公比 ,等差数列
,等差数列 满足
满足 .
. ,求数列
,求数列 的前n项和
的前n项和 .
.