题目内容
若数列 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 都有
都有 ,记
,记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)若 求证:对任意
求证:对任意 .
.
(1) ;(2)
;(2) ;(3)详见试题解析.
;(3)详见试题解析.
解析试题分析:(1)分别令 可求得
可求得 的值;(2)利用
的值;(2)利用 与
与 的关系式,先求
的关系式,先求 ,再利用已知条件
,再利用已知条件 求得数列
求得数列 的通项公式;(3)先利用累加法求得
的通项公式;(3)先利用累加法求得 ,再利用裂项相消法求和
,再利用裂项相消法求和 ,进而可证明不等式.
,进而可证明不等式.
试题解析:(1)由 ,得
,得 ,解得
,解得 . 1分
. 1分 ,得
,得 ,解得
,解得 . 3分
. 3分
(2)由 ①,
①,
当 时,有
时,有 ②, 4分
②, 4分
①-②得: , 5分
, 5分 数列
数列 是首项
是首项 ,公比
,公比 的等比数列 6分
的等比数列 6分 , 7分
, 7分 . 8分
. 8分
(3)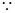
 ,
,
 , (1)
, (1) , (2)
, (2)
, ,
, , (
, ( ) 9分
) 9分
(1)+(2)+ +( )得
)得 , 10分
, 10分
 , 11分
, 11分 
 , 12分
, 12分

 , 13分
, 13分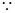
 ,
, 
 对任意
对任意 均成立. 14分
均成立. 14分
考点:1、数列通项公式的求法;2、数列前 项和的求法;3、数列不等式的证明.
项和的求法;3、数列不等式的证明.

练习册系列答案
相关题目
 上两点
上两点 ,若
,若 ,且P点的横坐标为
,且P点的横坐标为 .
. 求
求 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 都成立,试求a的取值范围.
都成立,试求a的取值范围. 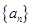 各项为非负实数,前n项和为
各项为非负实数,前n项和为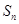 ,且
,且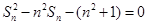
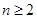 时,求
时,求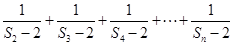 .
.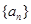 的前
的前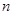 项和为
项和为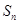 ,且
,且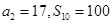 .
.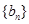 满足
满足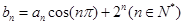 ,求数列
,求数列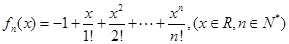
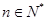 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;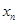 构成数列
构成数列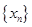 ,判断数列
,判断数列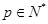 ,
,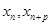 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与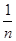 的大小.
的大小.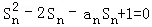 ,n=1,2,3
,n=1,2,3 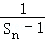 }是等差数列;
}是等差数列;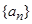 的前
的前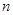 项和为
项和为 ,对任意
,对任意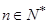 满足
满足 ,且
,且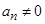 .
. ,求数列
,求数列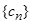 的前
的前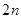 项和
项和 .
. 的前三项和为18,
的前三项和为18,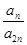 是一个与
是一个与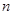 无关的常数,若
无关的常数,若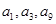 恰为等比数列
恰为等比数列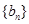 的前三项,(1)求
的前三项,(1)求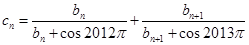 ,
,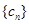 的前三
的前三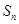 ,求证:
,求证:
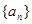 的公差
的公差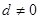 ,等比数列
,等比数列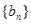 公比为
公比为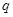 ,且
,且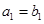 ,
,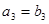 ,
,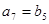
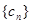 ,是否存在正整数
,是否存在正整数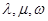 (其中
(其中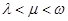 )使得
)使得 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组