题目内容
若无穷数列 满足:①对任意
满足:①对任意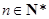 ,
,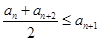 ;②存在常数
;②存在常数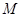 ,对任意
,对任意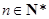 ,
,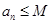 ,则称数列
,则称数列 为“
为“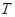 数列”.
数列”.
(Ⅰ)若数列 的通项为
的通项为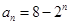
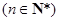 ,证明:数列
,证明:数列 为“
为“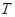 数列”;
数列”;
(Ⅱ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“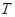 数列”,证明:对任意
数列”,证明:对任意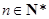 ,
,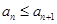 ;
;
(Ⅲ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“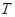 数列”,证明:存在
数列”,证明:存在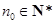 ,数列
,数列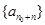 为等差数列.
为等差数列.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
解析试题分析:(Ⅰ)用作差法证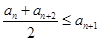 ,用单调性证
,用单调性证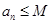 。(Ⅱ)用反证法证明。即假设存在正整数
。(Ⅱ)用反证法证明。即假设存在正整数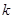 ,使得
,使得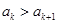 。根据
。根据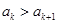 和
和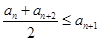 结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知
结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知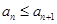 ,需分
,需分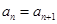 和
和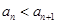 两种情况讨论,结合已知
两种情况讨论,结合已知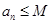 推理论证,根据等差的定义可证得存在
推理论证,根据等差的定义可证得存在 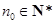 ,数列
,数列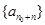 为等差数列.本题的关键是当
为等差数列.本题的关键是当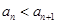 可变形得
可变形得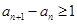 ,再用累加法表示
,再用累加法表示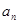 ,即
,即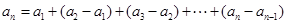 ,根据
,根据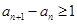 进行推理论证。
进行推理论证。
试题解析:(Ⅰ)证明:由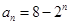 ,可得
,可得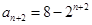 ,
, ,
,
所以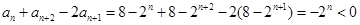 ,
,
所以对任意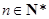 ,
,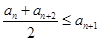 .
.
又数列 为递减数列,所以对任意
为递减数列,所以对任意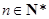 ,
,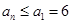 .
.
所以数列 为“
为“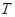 数列”. 5分
数列”. 5分
(Ⅱ)证明:假设存在正整数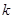 ,使得
,使得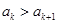 .
.
由数列 的各项均为正整数,可得
的各项均为正整数,可得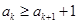 .
.
由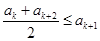 ,可得
,可得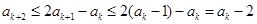 .
.
且 .
.
同理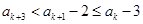 ,
,
依此类推,可得,对任意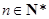 ,有
,有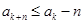 .
.
因为 为正整数,设
为正整数,设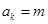 ,则
,则 .
.
在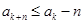 中,设
中,设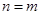 ,则
,则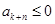 .
.
与数列 的各项均为正整数矛盾.
的各项均为正整数矛盾.
所以,对任意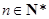 ,
,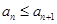 . 10分
. 10分
(Ⅲ)因为数列 为“
为“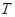 数列”,
数列”,
所以,存在常数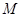 ,对任意
,对任意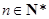 ,
,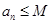 .
.
设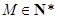 .
.
由(Ⅱ)可知,对任意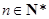 ,
,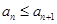 ,
,
则 .
.
若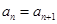 ,则
,则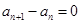 ;若
;若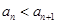 ,则
,则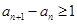 .
.
而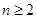 时,有
时,有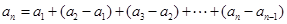 .
.
所以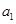 ,
,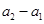 ,
,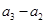 ,
,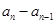 ,中最多有
,中最多有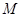 个大于或等于
个大于或等于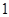 ,
,
否则与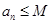 矛盾.
矛盾.
所以,存在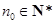 ,对任意的
,对任意的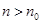 ,有
,有
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
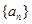 ,把
,把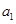 作为新数列
作为新数列 的第一项,把
的第一项,把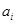 或
或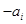 (
(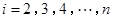 )作为新数列
)作为新数列 项,数列
项,数列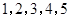 的一个生成数列是
的一个生成数列是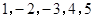 .已知数列
.已知数列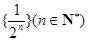 的生成数列,
的生成数列,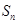 为数列
为数列 项和.
项和.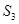 的所有可能值;
的所有可能值;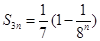 ,求数列
,求数列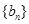 的通项公式;
的通项公式;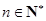 ,
,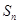 的所有可能值组成的集合为
的所有可能值组成的集合为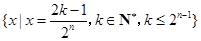 .
. ,
,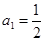 ,且满足
,且满足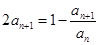 .
. 是等差数列;
是等差数列;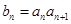 ,求数列
,求数列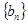 的前n项和
的前n项和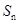 .
. 上两点
上两点 ,若
,若 ,且P点的横坐标为
,且P点的横坐标为 .
. 求
求 ;
; 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 都成立,试求a的取值范围.
都成立,试求a的取值范围. 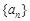 的首项
的首项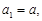 其中
其中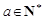 ,
,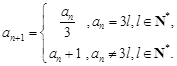 ,令集合
,令集合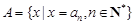 .
.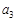 是数列
是数列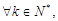 恒有
恒有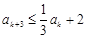 成立;
成立;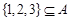 .
.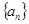 的前
的前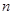 项和为
项和为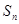 ,且
,且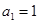 ,
,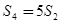 ,数列
,数列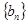 的前
的前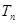 ,满足
,满足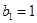 ,
,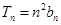 ,
,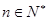 .
. 对所有的
对所有的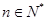 均成立,求实数
均成立,求实数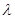 的取值范围.
的取值范围.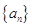 的前
的前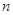 项和为
项和为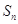 ,
,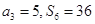 .
. 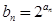 ,求数列
,求数列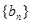 的前
的前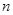 项和
项和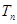 .
.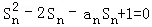 ,n=1,2,3
,n=1,2,3 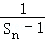 }是等差数列;
}是等差数列;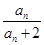 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(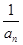 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )