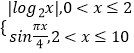题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.
(1)求抛物线C的方程;
(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求 ![]() 的最小值.
的最小值.
【答案】
(1)解:由题可知 ![]() ,则该直线方程为:
,则该直线方程为: ![]() ,
,
代入y2=2px(p>0)得: ![]() ,
,
设M(x1,y1),N(x2,y2),则有x1+x2=3p
∵|MN|=8,∴x1+x2+p=8,即3p+p=8,解得p=2
∴抛物线的方程为:y2=4x.

(2)解:设l方程为y=x+b,代入y2=4x,得x2+(2b﹣4)x+b2=0,
∵l为抛物线C的切线,∴△=0,
解得b=1,∴l:y=x+1
由(1)可知:x1+x2=6,x1x2=1
设P(m,m+1),则 ![]()
∴ ![]()
= ![]()
∵x1+x2=6,x1x2=1, ![]() ,y1y2=﹣4,
,y1y2=﹣4, ![]() ,
,
∴ ![]() ,
,
∴ ![]()
=2[m2﹣4m﹣3]=2[(m﹣2)2﹣7]≥﹣14
当且仅当m=2时,即点P的坐标为(2,3)时, ![]() 的最小值为﹣14.
的最小值为﹣14.
【解析】(1)过点F且斜率为1的直线代入抛物线,利用|MN|=8,可得x1+x2+p=8,即可求抛物线C的方程;(2)设l方程为y=x+b,代入y2=4x,利用直线l为抛物线C的切线,求出b,再利用向量的数量积公式求 ![]() ,利用配方法可求最小值.
,利用配方法可求最小值.

【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 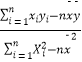 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.