Question

【题目】已知函数f（x）= ．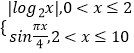
（1）设函数g（x）=f（x）﹣1，求函数g（x）的零点；
（2）若函数f（x1）=f（x2）=f（x3）=f（x4），且0＜x1＜x2＜x3＜x4≤10，求 的取值范围．

Answer 1

【答案】
（1）解：当0＜x≤2时，由|log2x|=1解得x=2或 ；

当2＜x≤10时，由 解得x=10，

∴函数g（x）有3个零点，分别为x=2， ．

（2）解：设f（x1）=f（x2）=f（x3）=f（x4）=a，由题意可知函数f（x）的图象与直线y=a交于四个不同的点．

在同一坐标系内作出两个函数的图象：

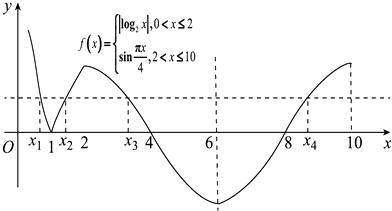
结合图象，由题意可知，x3+x4=12；

由|log2x1|=|log2x2|知，﹣log2x1=log2x2，即x1x2=1．

若函数f（x）的图象与直线y=a图象始终有四个交点，则2＜x3＜4．

故

因2＜x3＜4，所以， ．

所以， 的取值范围为（9，21）

【解析】（1）分类讨论，当0＜x≤2时，由|log2x|=1；当2＜x≤10时，由 ，即可求函数g（x）的零点；（2）画出函数f（x）的图象，确定x1x2=1，x3+x4=12，2＜x3＜x4＜10，由此可得则 的取值范围．