题目内容
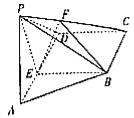
【题目】已知正三棱锥P﹣ABC底面边长为6，底边BC在平面α内，绕BC旋转该三棱锥，若某个时刻它在平面α上的正投影是等腰直角三角形，则此三棱锥高的取值范围是（ ） 
A.（0， 
]
B.（0， 
]∪[ ，3]
C.（0， ]
D.（0， ]∪[3， 
]
【答案】B
【解析】解：设正三棱锥P﹣ABC的高为h，
在△ABC中，设其中心为O，BC中点为E，则OE= 
× 
，
当h= 
时，PE= 
，PB= 
= 
，△PBC为等腰直角三角形，即当△PBC在平面α内时符合，
P不在平面α内时，设p在α内的投影为P'，PP'=d，∵△P'BC为等腰直角三角形，故P'E=3PE= 
＞3，
又PE= 
= 
＞3，
∴h2＞6，∴h＞ ．
由选项可知B符合，
故选：B．
【考点精析】关于本题考查的棱锥的结构特征，需要了解侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方才能得出正确答案．
练习册系列答案
天天练口算系列答案
相关题目
