题目内容
6.已知函数f(x)=loga(x+1),g(x)=loga(4-2x),a>0且a≠1.(1)求函数y=f(x)-g(x)的定义域;
(2)求使不等式f(x)>g(x)成立的实数x的取值范围;
(3)求函数y=2f(x)-g(x)-f(1)的零点.
分析 (1)根据对数函数的性质求出函数的定义域即可;
(2)通过讨论a的范围,得到关于x的不等式,求出不等式的解集即可;
(3)令y=0,得到关于x的方程,解出即可.
解答 解:(1)y=f(x)-g(x)=loga(x+1)-loga(4-2x),
由题意得:$\left\{\begin{array}{l}{x+1>0}\\{4-2x>0}\end{array}\right.$,解得:-1<x<2,
故函数的定义域是(-1,2);
(2)不等式f(x)>g(x),
即loga(x+1)>loga(4-2x),
0<a<1时,x+1<4-2x,解得:x<1,
而-1<x<2,故不等式的解集是(-1,1);
a>1时,x+1>4-2x,解得:x>1,
而-1<x<2,故不等式的解集是(1,2);
综上,0<a<1时,不等式的解集是(-1,1),
a>1时,不等式的解集是(1,2);
(3)令y=2f(x)-g(x)-f(1)=0,
即2loga(x+1)=loga(4-2x)+loga(1+1),
故(x+1)2=2(4-2x),解得:x=-7或x=1,
而-1<x<2,
故x=1.
点评 本题考查了对数函数的性质,考查函数的零点以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
15.已知z=m2-1+(m2-3m+2)i(m∈R,i为虚数单位),则“m=-1”是“z为纯虚数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有5个零点,则实数a的取值范围是( )
| A. | (-∞,-$\frac{1}{e}$) | B. | (-∞,-e) | C. | (e,+∞) | D. | ($\frac{1}{e}$,+∞) |
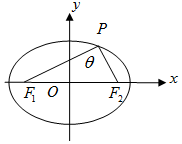 椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.
椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.