题目内容
16.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有5个零点,则实数a的取值范围是( )| A. | (-∞,-$\frac{1}{e}$) | B. | (-∞,-e) | C. | (e,+∞) | D. | ($\frac{1}{e}$,+∞) |
分析 先判断函数为偶函数,则要求函数f(x)有5个零点,只要求出当x>0时,f(x)有2个零点即可,分别y=ex与y=-ax的图象,利用导数的几何意义即可求出.
解答 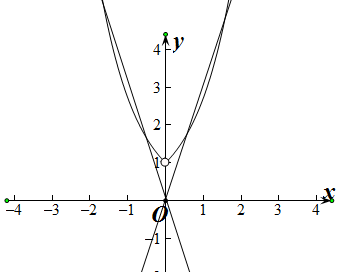 解:∵f(-x)=f(x),
解:∵f(-x)=f(x),
∴函数f(x)为偶函数,
∵当x=0,f(x)=0时,
∴要求函数f(x)有5个零点,
只要求出当x>0时,f(x)有2个零点即可,
分别y=ex与y=-ax的图象,如图所示,
设直线y=-ax与y=ex相切,
切点为(x0,y0),
∴y′=ex,
∴k=${e}^{{x}_{0}}$=$\frac{{e}^{{x}_{0}}}{{x}_{0}}$,
∴x0=1
∴-a=e,
∵当x>0时,f(x)有2个零点即可.
∴-a>e,
∴a<-e,
故选:B
点评 本题考查了函数零点的问题,以及函数的奇偶性,以及导数的几何意义,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
4.在下列抛物线中,其准线与(x-1)2+(y-2)2=9圆相切的是( )
| A. | x2=-8y | B. | y2=-8x | C. | y2=16x | D. | x2=4y |
1.微信是腾讯公司推出的一种手机通讯软件,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户为“A组”,否则为“B组”,调查结果如下:
(Ⅰ)根据以上数据,能否有60%的把握认为“A组”用户与“性别”有关?
(Ⅱ)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;(Ⅲ)从(Ⅱ)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中在“A组”的人数为X,试求X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(Ⅱ)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;(Ⅲ)从(Ⅱ)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中在“A组”的人数为X,试求X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
8.设函数f(x)=sin(2x+$\frac{π}{6}$),要得到g(x)=sin(2x+$\frac{2π}{3}$)的图象,可将f(x)的图象( )
| A. | 向左平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
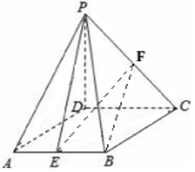 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E、F分别为AB和PC的中点,连接EF、BF.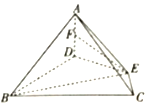 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.