题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，
•
=c2-（a-b）2，求cosC的值．
| CA |
| CB |
考点：余弦定理
专题：解三角形
分析：利用向量数量积运算可得：
•
=bacosC，再利用余弦定理即可得出．
| CA |
| CB |
解答：
解：∵
•
=bacosC，
•
=c2-（a-b）2，
∴bacosC=c2-a2-b2+2ab，
∴cosC=
=
，
解得cosC=
．
| CA |
| CB |
| CA |
| CB |
∴bacosC=c2-a2-b2+2ab，
∴cosC=
| a2+b2-c2 |
| 2ab |
| 2ab-abcosC |
| 2ab |
解得cosC=
| 2 |
| 3 |
点评：本题考查了向量数量积运算性质、余弦定理，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，一个底面半径为R的圆柱被与其底面所成角是30°的平面所截，截面是一个椭圆，则该椭圆的离心率是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知高为1的梯形ABCD内接于半径为1的圆O，若梯形的上底CD=1，则（
+
）•
=（ ）
| OA |
| OB |
| OC |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
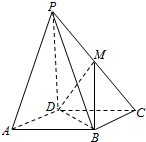在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是边长为2的正方形，且PD=AB．