题目内容
已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]()
(I)证明数列![]() 是等差数列,并求出数列
是等差数列,并求出数列![]() 的通项公式;
的通项公式;
(II)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 都成立的最大正整数
都成立的最大正整数![]() 的值。
的值。
(1)![]() (2)
(2)![]() 的最大值为18。
的最大值为18。
解析:
(1)由题意,当![]()
![]()
当![]()
![]()
则![]()
则![]()
即![]()
则数列![]() 是首项为1,公差为0的等差数列。
是首项为1,公差为0的等差数列。
从而![]() ,则数列
,则数列![]() 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
所以,![]()
(2)![]()
所以,![]()
![]()
由于![]()
因此![]() 单调递增,故
单调递增,故![]() 的最小值为
的最小值为![]()
令![]() ,所以
,所以![]() 的最大值为18。
的最大值为18。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
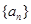 中,
中,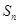 是
是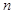 项和,且
项和,且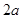 与
与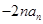 的等差中项,其中
的等差中项,其中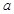 是不等于零的常数.
是不等于零的常数.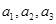 ; (2)猜想
; (2)猜想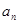 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.