题目内容
已知数列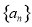 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有 成立,且
成立,且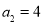 .
.
(1)求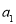 ,
,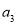 的值;
的值;
(2)猜想数列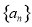 的通项公式,并给出证明.
的通项公式,并给出证明.
(1) ,
, (2)
(2)
【解析】
试题分析:(1)先列出 所满足条件
所满足条件 ,化简得
,化简得 ,再根据数列
,再根据数列 的各项均为正整数这一限制条件求出
的各项均为正整数这一限制条件求出 ,同理可得
,同理可得 (2)猜想:
(2)猜想: ,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得
,用数学归纳法证明的关键由k成立推出k+1成立,其推导思路同(1):由条件得 ,所以
,所以 ,所以
,所以 因为
因为 ,
, ,
, ,所以
,所以
试题解析:(1)因为 ,
,
当 时,由
时,由 ,即有
,即有 ,
,
解得 .因为
.因为 为正整数,故
为正整数,故 . 2分
. 2分
当 时,由
时,由 ,
,
解得 ,所以
,所以 . 4分
. 4分
(2)由 ,
, ,
, ,猜想:
,猜想: 5分
5分
下面用数学归纳法证明.
1当 ,
, ,
, 时,由(1)知
时,由(1)知 均成立. 6分
均成立. 6分
2假设 成立,则
成立,则 ,
,
由条件得 ,
,
所以 , 8分
, 8分
所以 9分
9分
因为 ,
, ,
, ,
,
又 ,所以
,所以 .
.
即 时,
时, 也成立.
也成立.
由1,2知,对任意 ,
, . 10分
. 10分
考点:数学归纳法

练习册系列答案
相关题目
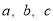 ,满足
,满足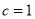 ,且
,且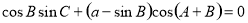 .
.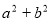 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值. 的零点为
的零点为 的零点为
的零点为 ,若
,若 可以是
可以是 B.
B.
 D.
D.
 ,被直线
,被直线 :
: 反射,反射光线通过点
反射,反射光线通过点 , 则反射光线所在直线的方程是 .
, 则反射光线所在直线的方程是 . 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 . 中,已知椭圆
中,已知椭圆 :
: ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
, .
.
 ,
, 互相垂直,求圆
互相垂直,求圆 ,
, ,求证:
,求证: ;
; 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由. ,被直线
,被直线 :
: 反射,反射光线通过点
反射,反射光线通过点 , 则反射光线所在直线的方程是 .
, 则反射光线所在直线的方程是 . ,
, ,并得到频率分布直方图(如图),已知测试平均成绩在区间
,并得到频率分布直方图(如图),已知测试平均成绩在区间 有20人.
有20人.
