题目内容
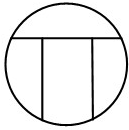 (2009•普陀区二模)园丁要用红、黄、蓝、白四种不同颜色的鲜花布置如图所示圆形花坛的四块区域.要求同一区域内须用同一种颜色的鲜花,相邻区域须用不同颜色的鲜花.设花圃中布置红色鲜花的区域数量为ξ,则随机变量ξ的数学期望Eξ
(2009•普陀区二模)园丁要用红、黄、蓝、白四种不同颜色的鲜花布置如图所示圆形花坛的四块区域.要求同一区域内须用同一种颜色的鲜花,相邻区域须用不同颜色的鲜花.设花圃中布置红色鲜花的区域数量为ξ,则随机变量ξ的数学期望Eξ1
1
.分析:花圃中红色鲜花区域的块数可能为0,1,2.求出相应的概率即可求得分布列及期望.
解答:解:随机变量ξ的取值分别为0,1,2.
则当ξ=0时,用黄、蓝、白三种颜色来涂色,
若左右为同色时,共有3×2×1=6种;
即ξ=0所包含的基本事件有6种,
所以P(ξ=0)=
=
;
P(ξ=2)=
=
;
所以P(ξ=1)=1-
-
=
.
∴E(ξ)=0×
+1×
+2×
=1.
故答案为:1
则当ξ=0时,用黄、蓝、白三种颜色来涂色,
若左右为同色时,共有3×2×1=6种;
即ξ=0所包含的基本事件有6种,
所以P(ξ=0)=
| 6 |
| 48 |
| 1 |
| 8 |
P(ξ=2)=
| 6 |
| 48 |
| 1 |
| 8 |
所以P(ξ=1)=1-
| 1 |
| 8 |
| 1 |
| 8 |
| 3 |
| 4 |
∴E(ξ)=0×
| 1 |
| 8 |
| 3 |
| 4 |
| 1 |
| 8 |
故答案为:1
点评:此题比较难,主要考查学生分析问题的能力,对学生的要求较高,属于中档题.

练习册系列答案
相关题目