题目内容
8.在复平面内,复数z对应的点是Z(1,-2),则复数z的共轭复数$\overline z$=( )| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
分析 由复数z对应的点是Z(1,-2),得z=1-2i,则复数z的共轭复数可求.
解答 解:由复数z对应的点是Z(1,-2),
得z=1-2i.
则复数z的共轭复数$\overline z$=1+2i.
故选:A.
点评 本题考查了复数的基本概念,是基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
18.若等比数列{an}的公比为q,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=2\\{a_2}x+{a_4}y=1\end{array}\right.$的解的情况下列说法正确的是( )
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当$q=\frac{1}{2}$时,方程组有无穷多解 | |
| D. | 当且仅当$q=\frac{1}{2}$时,方程组无解 |
16.一个几何体的三视图如图所示,则该几何体的体积为( )
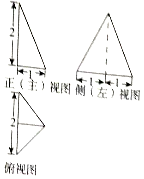

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
3.已知集合A={x|x2>x},B={-1,0,$\frac{1}{2}$,2},则A∩B=( )
| A. | {0,2} | B. | {-1,2} | C. | $\{0,\frac{1}{2}\}$ | D. | $\{\frac{1}{2},2\}$ |
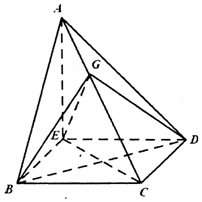 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD. 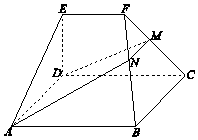 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.