题目内容
设f（x）是定义在R上的奇函数，且f（2）=0，当x＞0时，有xf′（x）-f（x）＜0恒成立，则不等式x2f（x）＞0的解集是 ．
考点：利用导数研究函数的单调性,函数单调性的性质
专题：导数的综合应用
分析：根据条件构造函数g（x）=
，利用函数的单调性和导数之间的关系，判断函数g（x）的单调性，然后根据函数f（x）的奇偶性判断函数f（x）的取值情况，即可求得不等式的解集．
| f(x) |
| x |
解答：
解：构造函数g（x）=
，g′（x）=
，
因为当x＞0时，有xf′（x）-f（x）＜0恒成立，即g′（x）=
＜0恒成立，
所以在（0，+∞）内g（x）单调递减．
因为f（2）=0，所以f（x）在（0，2）内恒有f（x）＞0；在（2，+∞）内恒有f（x）＜0．
又因为f（x）是定义在R上的奇函数，
所以在（-∞，-2）内恒有f（x）＞0；在（-2，0）内恒有f（x）＜0．
又不等式x2f（x）＞0的解集等价为不等式f（x）＞0的解集．
所以不等式的解集为（-∞，-2）∪（0，2）．
故答案为：（-∞，-2）∪（0，2）．
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
因为当x＞0时，有xf′（x）-f（x）＜0恒成立，即g′（x）=
| xf′(x)-f(x) |
| x2 |
所以在（0，+∞）内g（x）单调递减．
因为f（2）=0，所以f（x）在（0，2）内恒有f（x）＞0；在（2，+∞）内恒有f（x）＜0．
又因为f（x）是定义在R上的奇函数，
所以在（-∞，-2）内恒有f（x）＞0；在（-2，0）内恒有f（x）＜0．
又不等式x2f（x）＞0的解集等价为不等式f（x）＞0的解集．
所以不等式的解集为（-∞，-2）∪（0，2）．
故答案为：（-∞，-2）∪（0，2）．
点评：本题主要考查函数求导法则及函数单调性与导数的关系，同时考查了奇偶函数的图象特征．构造函数是解决本题的关键．
练习册系列答案
相关题目
正方形ABCD的边长是a，依次连接正方形ABCD各边中点得到一个新的正方形，再依次连接新正方形各边中点又得到一个新的正方形，依次得到一系列的正方形，如右图所示．现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个正方形的边逆时针方向爬行，如此下去，爬行了10条线段．则这10条线段的长度的平方和是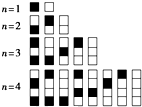
给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图所示：由此推断，当n=8时，黑色正方形互不相邻的着色方案共有已知函数f（x）=3x2+1，在x=1，△x=0.1时，△y的值为（ ）
| A、0.63 | B、0.21 |
| C、3.3 | D、0.3 |