题目内容
6.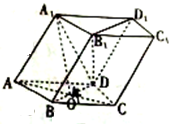 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.(1)证明:在侧棱AA1上存在-点E,使得0E⊥平面BB1D1D,并求出AE的长;
(2)求二面角A1一B1D-D1的余弦值.
分析 (1)根据条件,便可说明OB,OC,OA1三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系,然后求出空间一些点的坐标.可设在侧棱AA1上存在一点E,使得OE⊥平面BB1D1D,并且可以设E(0,$\frac{b}{2}-1$,b),并可以设平面BB1D1D的法向量为$\overrightarrow{m}=(x,y,z)$,从而可根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BD}=0}\\{\overrightarrow{m}•\overrightarrow{B{B}_{1}}=0}\end{array}\right.$求出法向量$\overrightarrow{m}$,从而有$\overrightarrow{OE}$∥$\overrightarrow{m}$,根据共线向量基本定理即可求出b的值,并且可以求出AE的长,这样便得出要证的结论正确;
(2)求二面角A1-B1D-D1的余弦值,可分别求出平面A1B1D和平面D1B1D的法向量,求法同上面求法向量的过程,然后求这两法向量夹角的余弦值即可得出二面角A1-B1D-D1的余弦值.
解答 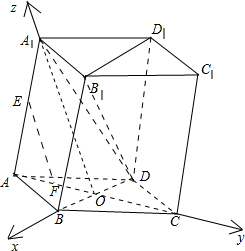 解:(1)证明:根据条件,A1O⊥底面ABCD,AC⊥BD;
解:(1)证明:根据条件,A1O⊥底面ABCD,AC⊥BD;
∴OB,OC,OA1三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则:
O(0,0,0),A(0,-1,0),B(2,0,0),C(0,1,0),D(-2,0,0),A1(0,0,2),B1(2,1,2),D1(-2,1,2);
∴$\overrightarrow{BD}=(-4,0,0),\overrightarrow{B{B}_{1}}=(0,1,2)$,设在侧棱AA1上存在点E,使OE⊥平面BB1D1D;
∵A1O⊥平面ABCD,A1O?平面A1AO;
∴平面A1AO⊥平面ABCD,过E作EF⊥AO,垂足为F,则EF⊥平面ABCD,且$\frac{EF}{AF}=\frac{{A}_{1}O}{AO}=\frac{2}{1}$;
∴设E(0,$\frac{b}{2}-1$,b),-1≤a≤0,0≤b≤2,$\overrightarrow{OE}=(0,\frac{b}{2}-1,b)$;
设平面BB1D1D的法向量为$\overrightarrow{m}=(x,y,z)$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BD}=-4x=0}\\{\overrightarrow{m}•\overrightarrow{B{B}_{1}}=y+2z=0}\end{array}\right.$;
取z=1,则$\overrightarrow{m}=(0,-2,1)$,则$\overrightarrow{m}$∥$\overrightarrow{OE}$;
存在k使,$\overrightarrow{OE}=k\overrightarrow{m}$;
∴(0,$\frac{b}{2}$-1,b)=(0,-2k,k);
∴$\left\{\begin{array}{l}{\frac{b}{2}-1=-2k}\\{b=k}\end{array}\right.$;
∴b=$\frac{2}{5}$;
∴$EF=\frac{2}{5},AF=\frac{1}{5}$,EF⊥AF;
∴$AE=\frac{\sqrt{5}}{5}$;
即在侧棱上存在一点E,使OE⊥平面BB1D1D,且AE=$\frac{\sqrt{5}}{5}$;
(2)设平面A1B1D的法向量为$\overrightarrow{p}=({x}_{1},{y}_{1},{z}_{1})$,$\overrightarrow{{A}_{1}{B}_{1}}=(2,1,0),\overrightarrow{{A}_{1}D}=(-2,0,-2)$,则:
$\left\{\begin{array}{l}{\overrightarrow{p}•\overrightarrow{{A}_{1}{B}_{1}}=2{x}_{1}+{y}_{1}=0}\\{\overrightarrow{p}•\overrightarrow{{A}_{1}D}=-2{x}_{1}-2{z}_{1}=0}\end{array}\right.$;
取x1=1,则$\overrightarrow{p}=(1,-2,-1)$;
同理设平面D1B1D的法向量为$\overrightarrow{q}=({x}_{2},{y}_{2},{z}_{2})$,根据$\left\{\begin{array}{l}{\overrightarrow{q}•\overrightarrow{{B}_{1}{D}_{1}}=0}\\{\overrightarrow{q}•\overrightarrow{{B}_{1}D}=0}\end{array}\right.$可求出$\overrightarrow{q}=(0,-2,1)$;
∴设二面角A1-B1D-D1的大小为θ,则cosθ=$\frac{\overrightarrow{p}•\overrightarrow{q}}{|\overrightarrow{p}||\overrightarrow{q}|}=\frac{3}{\sqrt{6}•\sqrt{5}}=\frac{\sqrt{30}}{10}$;
∴二面角A1-B1D-D1的余弦值为$\frac{\sqrt{30}}{10}$.
点评 考查面面垂直的判定定理,线面垂直的判定定理,以及菱形的对角线互相垂直,通过建立空间直角坐标系,利用空间向量解决线面垂直以及二面角等问题的方法,平面法向量的概念及其求法,共线向量基本定理,要清楚两平面法向量的夹角和两平面形成二面角的大小的关系.

| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 20 | D. | 5 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
| A. | $\sqrt{11}$,$\sqrt{13}$ | B. | 2$\sqrt{3}$,$\sqrt{14}$ | C. | $\sqrt{14}$,$\sqrt{15}$ | D. | $\sqrt{15}$,$\sqrt{17}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
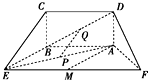 如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.
如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.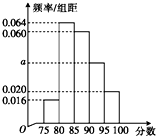 某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.
某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.