题目内容
1.在正四棱台ABCD-A1B1C1D1,AB=1,A1B1=3,AA1=4,这个正四棱台的高和斜高分别是( )| A. | $\sqrt{11}$,$\sqrt{13}$ | B. | 2$\sqrt{3}$,$\sqrt{14}$ | C. | $\sqrt{14}$,$\sqrt{15}$ | D. | $\sqrt{15}$,$\sqrt{17}$ |
分析 连结A1C1,AC,过点A1作A1E⊥平面ABCD,交AC于E,由勾股定理能求出这个正四棱台的高A1E;作A1F⊥AB,交AB于F,由勾股定理能求出这个正四棱台的斜高A1F.
解答 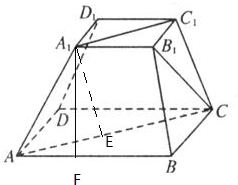 解:连结A1C1,AC,过点A1作A1E⊥平面ABCD,交AC于E,
解:连结A1C1,AC,过点A1作A1E⊥平面ABCD,交AC于E,
∵正四棱台ABCD-A1B1C1D1,AB=1,A1B1=3,AA1=4,
∴${A}_{1}{C}_{1}=\sqrt{2}$,$AC=3\sqrt{2}$,
∴AE=$\sqrt{2}$,
∴这个正四棱台的高A1E=$\sqrt{{4}^{2}-(\sqrt{2})^{2}}$=$\sqrt{14}$.
作A1F⊥AB,交AB于F,
由已知得AF=1,
∴这个正四棱台的斜高A1F=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$.
故选:C.
点评 本题考查正四棱台的高和斜高的求法,是基础题,解题时要认真审题,注意棱台的结构特征的合理运用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
11.目前我国很多城市出现了雾霾天气,已经给广大人民的健康带来影响,其中汽车尾气排放是造成雾霾天气的重要因素之一,很多城市提倡绿色出行方式,实施机动车尾号限行.某市为了解民众对“车辆限行”的态度,随机调查了50人,并半调查结果制成如表:
(1)若从年龄在[55,65)的被调查者中随机选取2人进行跟踪调查,求恰有1名不赞成“车辆限行”的概率;
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
参考公式和数据:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年,请根据上表完成2×2列联表,并说明民众对“车辆限行”的态度与年龄是否有关联.
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
12.已知程序框图如图所示,则该程序框图的功能是( )
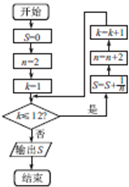

| A. | 求数列{$\frac{1}{n}$}的前11项和(n∈N*) | B. | 求数列{$\frac{1}{2n}$}的前11项和(n∈N*) | ||
| C. | 求数列{$\frac{1}{n}$}的前12项和(n∈N*) | D. | 求数列{$\frac{1}{2n}$的前12项和(n∈N*) |
9.已知直线3x+ay=0(a>0)被圆(x-2)2+y2=4所截得的弦长为2,则a的值为( )
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
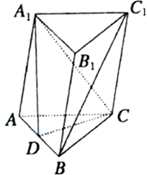 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.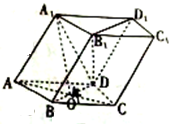 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.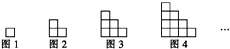 下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是136.
下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是136.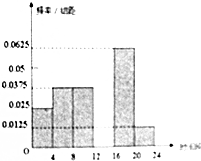 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题: