题目内容
11.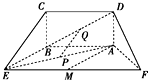 如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.
如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
分析 (1)连结AC,由三角形中位线定理得PQ∥EC,由此能证明PQ∥平面BCE.
(2)由已知得四边形ABEM为平行四边形,从而AM∥BE,且AM=BE=2.再由勾股定理得AM⊥AF.由此能证明AM⊥平面ADF.
解答 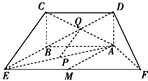 证明:(1)连结AC,如图所示:
证明:(1)连结AC,如图所示:
因为四边形ABCD是矩形,且Q为BD的中点,
所以Q为AC的中点.
又因为P为AE的中点,所以PQ∥EC,
又因为PQ?平面BCE,EC?平面BCE,所以PQ∥平面BCE.(7分)
(2)因为AB∥EM,且AB=EM=2$\sqrt{2}$,
所以四边形ABEM为平行四边形,
所以AM∥BE,且AM=BE=2.
在△AMF中,由AM=AF=2,MF=2$\sqrt{2}$,得AM2+AF2=MF2,故AM⊥AF.
由AD⊥平面ABEF,得AD⊥AM,
因为AD∩AF=A,所以AM⊥平面ADF.(14分)
点评 本题考查线面平行和线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
20.设△ABC的内角A,B,C所对的边长分别为a,b,c,且atanB=$\frac{20}{3}$,bsinA=4,则a等于( )
| A. | 3 | B. | $\frac{8}{3}$ | C. | 4 | D. | 5 |
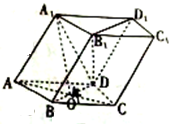 在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.
在四棱柱ABCD一A1B1C1D1中,底面ABCD是菱形,且AB=AA1=$\sqrt{5}$,BD=4,A1在底面 ABCD的射影是AC与BD的交点O.