题目内容
已知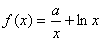 ,
, 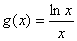 ,
,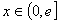 ,其中
,其中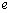 是无理数且
是无理数且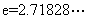 ,
,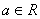 .
.
(1)若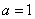 ,求
,求 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,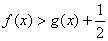 ;
;
(3)是否存在实数 ,使
,使 的最小值是
的最小值是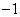 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:(1)当a=1时, ,
, ,
,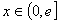
令 ,得x=1.
,得x=1.
当 时,
时, ,此时
,此时 单调递减;
单调递减;
当 时,
时, ,此时
,此时 单调递增.
单调递增.
所以 的单调递减区间为(0,1),单调递增区间为(1,e),
的单调递减区间为(0,1),单调递增区间为(1,e), 的极小值为
的极小值为 . (4分)
. (4分)
令 ,
,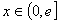 ,所以
,所以 .
.
当 时,
时, ,
, 在
在 上单调递增,
上单调递增,
所以 .
.
故在(1)的条件下,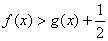 .
.
(3)假设存在实数a,使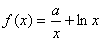 (
(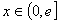 )有最小值-1.
)有最小值-1.
因为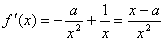 ,
,
①当 时,
时, ,
, 在
在 上单调递增,此时
上单调递增,此时 无最小值;
无最小值;
②当 时,当
时,当 时,
时, ,故
,故 在(0,a)单调递减;当
在(0,a)单调递减;当 时,
时, ,故
,故 在(a,e)单调递增;
在(a,e)单调递增;
所以 ,得
,得 ,满足条件;
,满足条件;
③当 时,因为
时,因为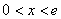 ,所以
,所以 ,故
,故 在
在 上单调递减.
上单调递减.
 ,得
,得 (舍去);
(舍去);
综上,存在实数 ,使得
,使得 在
在 上的最小值为-1.
上的最小值为-1.

练习册系列答案
相关题目
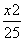 +
+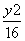 =1的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为___
=1的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为___
 ,观察下列各式:
,观察下列各式: ,
, ,
, ,...,类比有
,...,类比有 (
( ),则
),则 ( )
( )  B.
B. C.
C. D.
D.
 ,试求
,试求 为何值时,
为何值时,  为实数? (2)
为实数? (2) 则
则 是这个数列的( )
是这个数列的( )