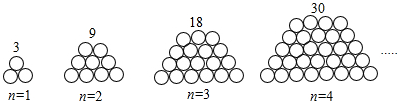
题目内容
10.设Sn为各项不相等的等差数列{an}的前n项和,已知a3a5=3a7,S3=9.(1)求数列{an}通项公式;
(2)设Tn为数列{${\frac{1}{{{a_n}{a_{n+1}}}}}$}的前n项和.
分析 (1)通过设{an}的公差为d,利用a3a5=3a7与S3=9联立方程组,进而可求出首项和公差,进而可得结论;
(2)通过(1)裂项、并项相加可知.
解答 解:(1)设{an}的公差为d,则由题意知$\left\{\begin{array}{l}({a_1}+2d)({a_1}+4d)=3({a_1}+6d)\\ 3{a_1}+\frac{3×2}{2}d=9\end{array}\right.$,
解得$\left\{\begin{array}{l}d=0\\{a_1}=3\end{array}\right.$(舍去)或$\left\{\begin{array}{l}d=1\\{a_1}=2\end{array}\right.$,
∴an=2+(n-1)×1=n+1.
(2)∵$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,
∴${T_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$
=$(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})++(\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{1}{2}-\frac{1}{n+2}=\frac{n}{2(n+2)}$.
即Tn=$\frac{n}{2(n+2)}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,涉及基本不等式等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知集合A={x|-2<x<2},B={x|(x+1)(x-3)≤0},则A∩(∁RB)=( )
| A. | (-1,2) | B. | (-2,-1] | C. | (-2,-1) | D. | (2,3) |
 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,且$A({\frac{π}{2},1}),B({π,-1})$,则φ值为-$\frac{5π}{6}$.
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,且$A({\frac{π}{2},1}),B({π,-1})$,则φ值为-$\frac{5π}{6}$.