题目内容

17．某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1，2，3，4四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（　　）
A．乙，丁B．甲，丙C．甲，丁D．乙，丙

分析 根据题意，假设乙的说法是正确的，分析可得丁也是正确的，那么甲丙的说法都是错误的，分析可得乙的说法相矛盾，即可得假设乙的说法是正确是错误的，从而可得丁的说法也是错误的，从而可得说法正确的是甲、丙，即可得答案．

解答 解：根据题意，由于甲乙丙丁四人中有且只有两人的说法是正确的，
假设乙的说法是正确的，则丁也是正确的，那么甲丙的说法都是错误的，
如果丙同学说：“1班、4班中有且只有一个班获奖”是错误的，那么1班、4班都获奖或1班、4班都没有获奖，与乙的说法矛盾，
故乙的说法是错误，则丁同学说：“乙说得对”也是错误的；
故说法正确的是甲、丙，
故选：B．

点评 本题考查合情推理的运用，此类题目常用的手段是假设法，抓住题干中的条件进行推理，推理所得的结果如果不互相矛盾，则假设成立，反之，不成立．

练习册系列答案
相关题目
7．如图，已知菱形ABCD与直角梯形ABEF所在的平面互相垂直，其中BE∥AF，AB⊥AF，AB=BE=$\frac{1}{2}$AF=2，∠CBA=$\frac{π}{3}$，P为DF的中点．
（Ⅰ）求证：PE∥平面ABCD
（Ⅱ）求二角D-EF-A的余弦值；
（Ⅲ）设G为线段AD上一点，$\overrightarrow{AG}=λ\overrightarrow{AD}$，若直线FG与平面ABEF所成角的正弦值为$\frac{\sqrt{39}}{26}$，求AG的长．
8．已知三棱锥S-ABC，满足SA⊥SB，SB⊥SC，SC⊥SA，且SA=SB=SC=3，则该三棱锥外接球的表面积为（　　）
A．4$\sqrt{3}$πB．$\frac{27\sqrt{3}π}{2}$C．27πD．9π
5．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，F为椭圆C的右焦点，过点F作x轴的垂线交椭圆C于一点$E（{1，\frac{3}{2}}）$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知A，B为椭圆C的左右顶点，P为椭圆C上异于A，B的任意一点，直线AP、BP分别交直线l：x=m（m＞a）于M，N两点，
（ⅰ）设直线AP、BP的斜率分别为k1，k2，求证：k1k2为定值；
（ⅱ）若以线段MN为直径的圆过点F，求实数m的值．
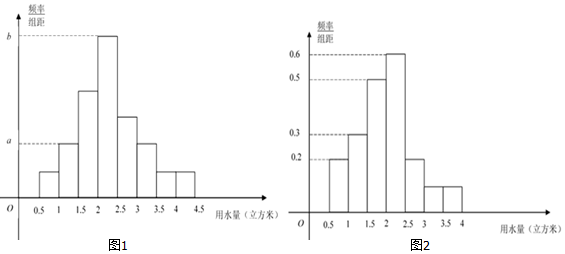
12．某校学生在进行“南水北调工程对北京市民的影响”的项目式学习活动中，对某居民小区进行用水情况随机抽样调查，获得了该小区400位居民某月的用水量数据（单位：立方米），整理得到如下数据分组及频数分布表和频率分布直方图（图1）：
组号分组频数
1[0.5，1）20
2[1，1.5）40
3[1.5，2）80
4[2，2.5）120
5[2.5，3）60
6[3，3.5）40
7[3.5，4）20
8[4，4.5）20
（Ⅰ）求a，b的值；
（Ⅱ）从该小区随机选取一名住户，试估计这名住户一个月用水量小于3立方米的概率；
（Ⅲ）若小区人均月用水量低于某一标准，则称该小区为“节水小区”．假设同组中的每个数据用该组区间的右端点值代替，经过估算，该小区未达到“节水小区”标准，而且该小区居民月用水量不高于这一标准的比例为65%，经过同学们的节水宣传，三个月后，又进行一次同等规模的随机抽样调查，数据如图2所示，估计这时小区是否达到“节水小区”的标准？并说明理由．
2．6个学生站成一排，学生甲与学生乙相邻，学生甲与学生丙不相邻，则不同的排法有192．
3．已知Sn是等差数列{an}的前n项和，若a1=-2017，$\frac{{{S_{2014}}}}{2014}-\frac{{{S_{2008}}}}{2008}$=6，则S2017=-2017．
20．函数$y=\frac{{{x^2}+7x+10}}{x+1}（{x＞-1}）$的最小值为（　　）
A．2B．7C．9D．10
1．已知数列{an}中，a1=3，a2=6，an+2=an+1-an，则a2016=（　　）
A．6B．-6C．3D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网