题目内容
12.已知数列{an}的前n项和Sn=(-1)n-1•n,若对任意的正整数n,有(an+1-p)(an-p)<0恒成立,则实数p的取值范围是(-3,1).分析 Sn=(-1)n-1•n,可得:a1=S1=1.当n≥2时,an=Sn-Sn-1,可得an=(-1)n-1(2n-1),对n分类讨论,利用(an+1-p)(an-p)<0恒成立,即可解出.
解答 解:∵Sn=(-1)n-1•n,
∴a1=S1=1.
当n≥2时,an=Sn-Sn-1=(-1)n-1•n-(-1)n-2(n-1)=(-1)n-1(2n-1),当n=1时也成立,
∴an=(-1)n-1(2n-1),
当n为偶数时,(an+1-p)(an-p)<0化为:[(2n+1)-p][-(2n-1)-p]<0,-(2n-1)<p<2n+1,可得-3<p<5.
当n为奇数时,(an+1-p)(an-p)<0化为:[-(2n+1)-p][(2n-1)-p]<0,-(2n+1)<p<2n-1,可得-3<p<1.
∴$\left\{\begin{array}{l}{-3<p<5}\\{-3<p<1}\end{array}\right.$,
解得-3<p<1.
故答案为:(-3,1).
点评 本题考查了递推公式、不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.在数列{an}中,已知${S_n}={2^n}-1$,则a12+a22+…+an2等于( )
| A. | $\frac{{4}^{n}-1}{3}$ | B. | $\frac{({2}^{n}-1)^{2}}{3}$ | C. | 4n-1 | D. | (2n-1)2 |
20.已知集合M={y|y=2sinx,x∈R},N={x|y=lgx},则M∩N为( )
| A. | [-2,2] | B. | (0,+∞) | C. | (0,2] | D. | [0,2] |
17.已知等差数列{an}的前n项和为Sn,a1=-7,S8=0.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
4.已知定义在R上的偶函数f(x),满足f(x+4)=f(x),f(x)=sinπx+2|sinπx|,x∈[0,2],函数g(x)=f(x)-loga(x+$\frac{3}{2}$),若以g(x)=0在区间[-1,3]上至少6个根,则a的取值范围为( )
| A. | [${4}^{\frac{1}{3}}$,+∞) | B. | [${4}^{\frac{1}{3}}$,6] | C. | [4,+∞) | D. | [3,4] |
2.已知命题p;$\frac{1}{2}$≤x≤1,命题q:(x-a)(x-a-1)≤0,若¬p是¬q的必要不充分条件,则实数a的取值范围是( )
| A. | [0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{3}$,$\frac{1}{2}$] | D. | $(\frac{1}{3},\frac{1}{2}]$ |
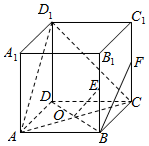 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.