题目内容
【题目】已知椭圆![]() ,四点
,四点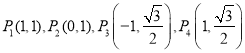 中恰有三点在椭圆上.
中恰有三点在椭圆上.
(1)求椭圆C的方程
(2)椭圆C上是否存在不同的两点M,N关于直线![]() 对称?若存在,请求出直线MN的方程,若不存在,请说明理由.
对称?若存在,请求出直线MN的方程,若不存在,请说明理由.
(3)设直线l不经过点![]() 且与C相交于A,B两点,若直线
且与C相交于A,B两点,若直线![]() 与直线
与直线![]() 的斜率之和为1,求证直线l必过定点,并求出这个定点坐标.
的斜率之和为1,求证直线l必过定点,并求出这个定点坐标.
【答案】(1)![]() (2)存在,
(2)存在,![]() (3)证明见解析,
(3)证明见解析,![]()
【解析】
(1)根据对称性得到 在椭圆上,故
在椭圆上,故![]() 不在椭圆上,代入数据计算得到答案.
不在椭圆上,代入数据计算得到答案.
(2)假设存在,设![]() ,代入椭圆相减得到
,代入椭圆相减得到![]() ,再根据
,再根据![]() 计算得到答案.
计算得到答案.
(3)设![]() ,利用韦达定理得到
,利用韦达定理得到 ,根据斜率之和为1得到
,根据斜率之和为1得到![]() ,得到过定点
,得到过定点![]()
(1)根据对称性知 在椭圆上,故
在椭圆上,故![]() 不在椭圆上.
不在椭圆上.
代入![]() 得到
得到![]() ,代入
,代入 得到
得到![]()
故椭圆方程为:![]()
(2)存在;假设存在,设![]() ,代入椭圆相减得到:
,代入椭圆相减得到:
![]()
设![]() 中点为
中点为![]() ,则
,则![]()
![]() 在直线
在直线![]() 上,得到
上,得到![]() ,解得
,解得![]()
故![]() 方程为
方程为![]()
(3)设![]() ,联立方程得到
,联立方程得到 故
故![]()
故
![]()
故直线方程为![]() 过定点
过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】上海市普通高中学业水平等级考成绩共分为五等十一级,各等级换算成分数如表所示:
等级 |
| A |
| B |
|
| C |
|
| D | E |
分数 | 70 | 67 | 64 | 61 | 58 | 55 | 52 | 49 | 46 | 43 | 40 |
上海某高中2018届高三![]() 班选考物理学业水平等级考的学生中,有5人取得
班选考物理学业水平等级考的学生中,有5人取得![]() 成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人
成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人![]()