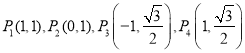题目内容
【题目】下列四个命题:
①若
，
，则
②函数
，的最小值是3
③用长为
的铁丝围成--个平行四边形，则该平行四边形能够被直径为
的圆形纸片完全覆盖
④已知正实数
，
满足
，则
的最小值为
.
其中所有正确命题的序号是__________．
【答案】①③④
【解析】
①利用不等式的性质即可得出；
②取特殊值可排除②；
③利用余弦定理及基本不等式判断；
④利用基本不等式可证．
解：对于①，
，
．
，
，
，
，
，
同除
得
同除
得
综上得
，故①正确；
对于②，
则
，故②错误；
对于③，设平行四边形的一组邻边分别为
夹角为
，
，
则对角线为
所以平行四边形的任何一边及对角线都小于
，该平行四边形能够被直径为的圆形纸片完全覆盖，故③正确；
对于④，正实数
，
满足
，则
，
所以
当且仅当
即
取等号，故④正确；
故答案为:①③④
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
